Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find minimum cost to connect each Cartesian coordinates in C++
Suppose we have a list of 2D Cartesian coordinate points (x, y). We can connect (x0, y0) and (x1, y1), whose cost is |x0 - x1| + |y0 - y1|. If we are allowed to connect any number of points, we have to find the minimum cost necessary such that every point is connected by a path.
So, if the input is like points = [[0, 0],[0, 2],[0, -2],[2, 0],[-2, 0], [2, 3], [2, -3]],
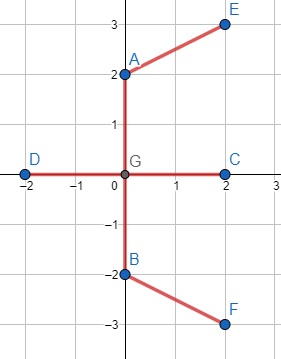
then the output will be 14 because, from (0, 0) to (0, 2),(0, -2),(2, 0),(-2, 0), costs are 2, total is 8, and (2, 3) is nearest from (0, 2), cost is |2+1| = 3 and for (2, -3) it is nearest to (0, -2), cost is also 3. so total cost is 8 + 6 = 14.
To solve this, we will follow these steps −
- MAX := inf
- Define a function interval(), this will take i, j, and points array p,
- return |(p[i, x] - p[j, x]) + |p[i, y] - p[j, y]||
- From the main method, do the following −
- n := size of p
- if n < 2, then: return 0
- Define an array called distance with n slots and fill with MAX
- Define an array visited of size n
- distance[0] := 0
- for initialize i := 0, when i < n, update (increase i by 1), do −
- min_d := MAX
- node := 0
- for initialize j := 0, when j < n, update (increase j by 1), do −
- if visited[j] is false and distance[j] < min_d, then −
- min_d := distance[j]
- node := j
- if visited[j] is false and distance[j] < min_d, then −
- visited[node] := true
- cost := cost + distance[node]
- for initialize j := 0, when j < n, update (increase j by 1), do −
- if visited[j] is false, then −
- d := interval(node, j, p)
- distance[j] := minimum of distance[j] and d
- if visited[j] is false, then −
- return cost
Example
Let us see the following implementation to get better understanding −
#include <iostream>
#include <vector>
#define MAX 99999
using namespace std;
int interval(int i, int j, vector<vector<int>>& p) {
return abs(p[i][0] - p[j][0]) + abs(p[i][1] - p[j][1]);
}
int solve(vector<vector<int>>& p) {
int n = p.size(), cost = 0;
if (n < 2) return 0;
vector<int> distance(n, MAX);
vector<bool> visited(n);
distance[0] = 0;
for (int i = 0; i < n; i++) {
int min_d = MAX, node = 0;
for (int j = 0; j < n; j++) {
if (!visited[j] && distance[j] < min_d) {
min_d = distance[j];
node = j;
}
}
visited[node] = true;
cost += distance[node];
for (int j = 0; j < n; j++) {
if (!visited[j]) {
int d = interval(node, j, p);
distance[j] = min(distance[j], d);
}
}
}
return cost;
}
int main(){
vector<vector<int>> points = {{0, 0},{0, 2},{0, -2},{2, 0},{-2, 0}, {2, 3}, {2, -3}};
cout << solve(points);
}Input
{{0, 0},{0, 2},{0, -2},{2, 0},{-2, 0}, {2, 3}, {2, -3}}Output
14
Updated on: 16-Oct-2021
169 Views
Advertisements