Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find minimum cost to connect all points in Python
Suppose we have an array called points with some points in the form (x, y). Now the cost of connecting two points (xi, yi) and (xj, yj) is the Manhattan distance between them, the formula is |xi - xj| + |yi - yj|. We have to find the minimum cost to make all points connected.
So, if the input is like points = [(0,0),(3,3),(2,10),(6,3),(8,0)], then the output will be 22 because
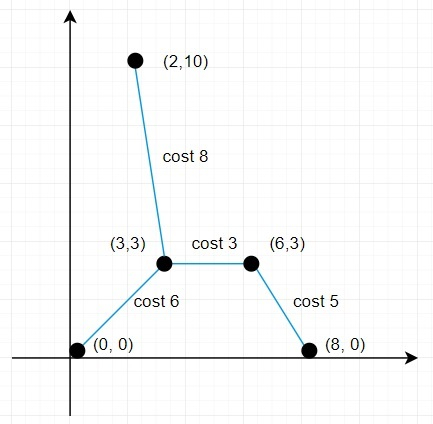
so here total distance is (6+5+3+8) = 22.
To solve this, we will follow these steps −
- points_set := a new set holding numbers from range 0 to size of points - 1
- heap := make a heap with pair (0, 0)
- visited_node := a new set
- total_distance := 0
- while heap is not empty and size of visited_node < size of points, do
- (distance, current_index) := delete element from heap
- if current_index is not present in visited_node, then
- insert current_index into visited_node
- delete current_index from points_set
- total_distance := total_distance + distance
- (x0, y0) := points[current_index]
- for each next_index in points_set, do
- (x1, y1) := points[next_index]
- insert (|x0 - x1| + |y0 - y1| , next_index) into heap
- return total_distance
Example
Let us see the following implementation to get better understanding −
import heapq def solve(points): points_set = set(range(len(points))) heap = [(0, 0)] visited_node = set() total_distance = 0 while heap and len(visited_node) < len(points): distance, current_index = heapq.heappop(heap) if current_index not in visited_node: visited_node.add(current_index) points_set.discard(current_index) total_distance += distance x0, y0 = points[current_index] for next_index in points_set: x1, y1 = points[next_index] heapq.heappush(heap, (abs(x0 - x1) + abs(y0 - y1), next_index)) return total_distance points = [(0,0),(3,3),(2,10),(6,3),(8,0)] print(solve(points))
Input
[(0,0),(3,3),(2,10),(6,3),(8,0)]
Output
22
Updated on: 04-Oct-2021
333 Views
Advertisements