Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Print all the cycles in an undirected graph in C++
In this problem, we are given an undirected graph and we have to print all the cycles that are formed in the graph.
Undirected Graph is a graph that is connected together. All the edges of the unidirectional graph are bidirectional. It is also known as an undirected network.
Cycle in a graph data structure is a graph in which all vertices form a cycle.
Let’s see an example to understand the problem better −
Graph-
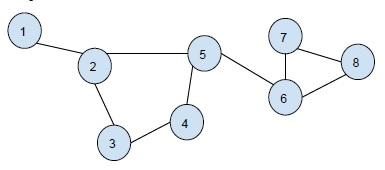
Output-
Cycle 1: 2 3 4 5 Cycle 2: 6 7 8
For this, we will make use of a few properties of the graph. You need to use graph coloring method and color all the vertices which occur in a cyclic graph. Also, if a vertex is partially visited, it will give rise to a cyclic graph. So, we will color this vertex and all next vertex till the same is reached again.
ALGORITHM
Step 1: call DFS traversal for the graph which can color the vertices. Step 2: If a partially visited vertex is found, backtrack till the vertex is reached again and mark all vertices in the path with a counter which is cycle number. Step 3: After completion of traversal, iterate for cyclic edge and push them into a separate adjacency list. Step 4: Print the cycles number wise from the adjacency list.
Example
#include <bits/stdc++.h>
using namespace std;
const int N = 100000;
vector<int> graph[N];
vector<int> cycles[N];
void DFSCycle(int u, int p, int color[], int mark[], int par[], int& cyclenumber){
if (color[u] == 2) {
return;
}
if (color[u] == 1) {
cyclenumber++;
int cur = p;
mark[cur] = cyclenumber;
while (cur != u) {
cur = par[cur];
mark[cur] = cyclenumber;
}
return;
}
par[u] = p;
color[u] = 1;
for (int v : graph[u]) {
if (v == par[u]) {
continue;
}
DFSCycle(v, u, color, mark, par, cyclenumber);
}
color[u] = 2;
}
void insert(int u, int v){
graph[u].push_back(v);
graph[v].push_back(u);
}
void printCycles(int edges, int mark[], int& cyclenumber){
for (int i = 1; i <= edges; i++) {
if (mark[i] != 0)
cycles[mark[i]].push_back(i);
}
for (int i = 1; i <= cyclenumber; i++) {
cout << "Cycle " << i << ": ";
for (int x : cycles[i])
cout << x << " ";
cout << endl;
}
}
int main(){
insert(1, 2);
insert(2, 3);
insert(3, 4);
insert(4, 5);
insert(5, 2);
insert(5, 6);
insert(6, 7);
insert(7, 8);
insert(6, 8);
int color[N];
int par[N];
int mark[N];
int cyclenumber = 0;
cout<<"Cycles in the Graph are :\n";
int edges = 13;
DFSCycle(1, 0, color, mark, par, cyclenumber);
printCycles(edges, mark, cyclenumber);
}Output
Cycles in the Graph are −
Cycle 1: 2 3 4 5 Cycle 2: 6 7 8
2K+ Views
To Continue Learning Please Login