Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Sum of the minimum elements in all connected components of an undirected graph in C++
In this problem, we are given an array arr of N numbers where arr[i] represents (i+1)th node. Also, there are M pairs of edges where u and v represent the node connected by the edge. Our task is to create a program to find the sum of the minimum elements in all connected components of an undirected graph. If a node has no connectivity to any other node, count it as a component with one node.
Let’s take an example to understand the problem,
Input
arr[] = {2, 7, 5, 1, 2} m = 2
1 2
4 5Output
8
Explanation
Below is the graph depicted above −
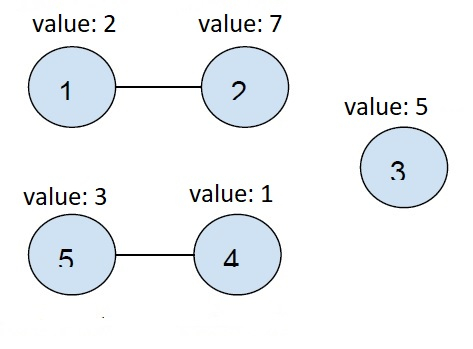
We have two connected nodes and one single node
So, let’s take the minimum of all connected components
Min (node1 and node2) = min (2, 7) = 2
Min (node4 and node5) = min (1, 3) = 1
Min (node3) = min (5) = 5
Sum = 1 + 2 + 5 = 8
To solve this problem, we will find all connected nodes of the undirected graph using any of the traversal techniques (BFS or DFS) and then create a visited array for all nodes that are visited for that no double visit is not there. On visiting connected nodes that are connected directly or indirectly, we will find the minimum of all connections. And add this minimum value of thesum variable. After we have visited all the nodes, we will print the sum.
Example
Program to illustrate the working of our solution,
#include <bits/stdc++.h>
using namespace std;
const int N = 100;
vector<int> graph[N];
bool visited[N];
void dfs(int node, int arr[], int minimum){
minimum = min(minimum, arr[node]);
visited[node] = true;
for (int i : graph[node]) {
if (!visited[i])
dfs(i, arr, minimum);
}
}
void createEdge(int u, int v){
graph[u - 1].push_back(v - 1);
graph[v - 1].push_back(u - 1);
}
int minSum(int arr[], int n){
int sum = 0;
for (int i = 0; i < n; i++) {
if (!visited[i]) {
int minimum = arr[i];
dfs(i, arr, minimum);
sum += minimum;
}
}
return sum;
}
int main(){
int arr[] = {2, 7, 5, 1, 3};
createEdge(1, 2);
createEdge(4, 5);
int n = sizeof(arr) / sizeof(arr[0]);
cout<<"The sum of minimum elements in all connected components of an undirected graph is ";
cout<<minSum(arr, n);
return 0;
}Output
The sum of minimum elements in all connected components of an undirected graph is 8
309 Views
