Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Product of lengths of all cycles in an undirected graph in C++
We are given with the undirected as well as unweighted graph as an input and the task is to find the product of the cycles that are formed in the given and display the result.
Example
Input
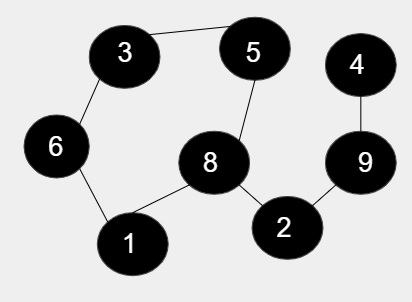
In the given figure, there are 8 nodes and out of that 5 nodes are forming cycle including 1, 6, 3, 5, 8 and rest of the node are not included in the cycle. So, the length of the cycle is 5 as it includes 5 node therefore product is 5
In the given figure, there are 12 nodes and out of that 11(5 +6) nodes are forming cycle including 1, 6, 3, 5, 8 and 9, 4, 10, 11, 22, 12 and the rest of the node 2 is not included in the cycle. So, the length of the cycle is 5 * 6 = 30
Approach used in the below program is as follows−
- Input the nodes for forming the cycle
- Create the DFS function and call it to traverse the vertex by coloring it
- Either the node are marked completely visited or partially visited
- Completely visited node need not be visit again and hence need not to store it whereas partially visited nodes need to be stored because they are visited again
- Print the result
Algorithm
Start Step 1-> declare function to traverse the graph using DFS approach void DFS(int i, int j, int color[], int highlight[], int parent[], int& number) IF color[i] = 2 Return End IF color[i] = 1 Set number++ Declare and set int temp = j Set highlight[temp] = number Loop While temp != i Set temp = parent[temp] Set highlight[temp] = number End Return End Set parent[i] = j Set color[i] = 1 For int k : graph[i] IF k = parent[i] Continue End Call DFS(k, i, color, highlight, parent, number) End Set color[i] = 2 Step 2-> declare function to find product of nodes in cycle int product(int edge, int highlight[], int& number) call unordered_map<int, int> mp Loop For i = 1 and i <= edge and i++ IF (highlight[i] != 0) Set mp[highlight[i]]++ End End Declare and set int temp = 1 Loop For i = 1 and i <= number and i++ Set temp = temp * mp[i] End IF number = 0 Set temp = 0 End return temp Step 3-> In main() Call function as insert(1, 2) to insert a node Declare int color[size], parent[size] Declare int highlight[size] Declare and set int number = 0 Declare and set int edge = 10 Call DFS(1, 0, color, highlight, parent, number) Call print function as product(edge, highlight, number) Stop
Example
#include <bits/stdc++.h>
using namespace std;
const int size = 100000;
vector<int> graph[size];
//function to traverse the graph using DFS approach
void DFS(int i, int j, int color[], int highlight[], int parent[], int& number) {
// for travered node
if (color[i] == 2) {
return;
}
//not completely visited
if (color[i] == 1) {
number++;
int temp = j;
highlight[temp] = number;
//for backtracking the vertex
while (temp != i) {
temp = parent[temp];
highlight[temp] = number;
}
return;
}
parent[i] = j;
color[i] = 1;
for (int k : graph[i]) {
if (k == parent[i]) {
continue;
}
DFS(k, i, color, highlight, parent, number);
}
color[i] = 2;
}
// function for inserting edges to graph
void insert(int u, int v) {
graph[u].push_back(v);
graph[v].push_back(u);
}
// Find product of nodes in cycle
int product(int edge, int highlight[], int& number) {
unordered_map<int, int> mp;
for (int i = 1; i <= edge; i++) {
if (highlight[i] != 0)
mp[highlight[i]]++;
}
int temp = 1;
for (int i = 1; i <= number; i++) {
temp = temp * mp[i];
}
if (number == 0)
temp = 0;
return temp;
}
int main() {
//for inserting a node in the graph
insert(1, 2);
insert(2, 3);
insert(3, 4);
insert(4, 6);
insert(4, 7);
insert(5, 6);
insert(3, 5);
insert(7, 8);
insert(6, 10);
insert(5, 9);
insert(10, 11);
int color[size], parent[size];
int highlight[size];
int number = 0;
int edge = 10;
DFS(1, 0, color, highlight, parent, number);
// function to print the cycles
cout<<"product of all the nodes in the cycle is :"<< product(edge, highlight, number);
return 0;
}Output
Product of all the nodes in the cycle is :4
Updated on: 23-Dec-2019
164 Views
Advertisements