Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Find if an undirected graph contains an independent set of a given size in C++
Concept
With respect of a given undirected graph, verify if it contains an independent set of size l. If there exists an independent set of size l print ‘Yes’, else print ‘No’. It should be noted that an independent set in a graph is defined as a set of vertices which are not directly connected to each other.
Input
L = 4, graph = [[1, 0, 1, 0, 0], [0, 1, 1, 0, 0],[1, 1, 1, 1, 1], [0, 0, 1, 1, 0],[0, 0, 1, 0, 1]];
Output
Yes
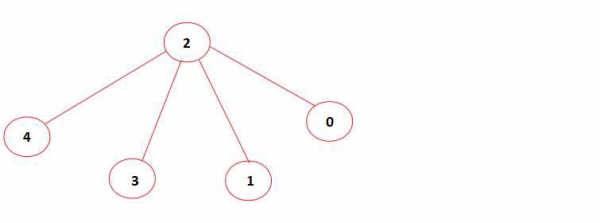
The above graph contains an independent set of size 4 (vertices 0, 1, 3, 4 are not directly connected to each other). Hence the output is ‘Yes’.
Input
L = 4, graph =[[1, 1, 1, 0, 0],[1, 1, 1, 0, 0],[1, 1, 1, 1, 1],[0, 0, 1, 1, 0],[0, 0, 1, 0, 1]];
Output
No
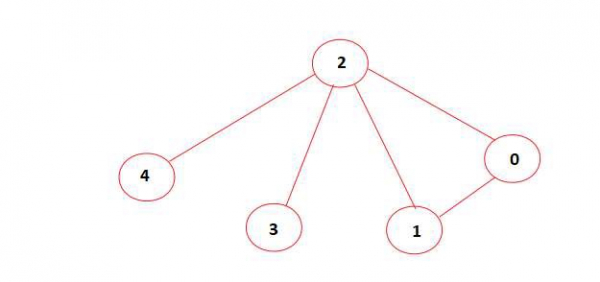
In the diagram, the above graph doesn’t contain an independent set of size 4. Hence output is ‘No’.
Method
- At first, initialize a variable sol with boolean False value.
- Determine all the possible sets of vertices of size L from the given graph.
- It has been seen that if an independent set of size l is found, change the value of sol to True and return.
- Otherwise continue checking for other possible sets.
- At last, if sol is True, print ‘Yes’ else print ‘No’.
Example
// C++ code to check if a given graph
// contains an independent set of size k
#include <bits/stdc++.h>
using namespace std;
// Shows function prototype
bool check1(int[][5], vector<int>&, int);
// Shows function to construct a set of given size l
bool func(int graph1[][5], vector<int>&arr1,
int l, int index1, bool sol1[]){
// Verify if the selected set is independent or not.
// Used to change the value of sol to True and return
// if it is independent
if (l == 0){
if (check1(graph1, arr1, arr1.size())){
sol1[0] = true;
return true;
}
}
else{
// Now set of size l can be formed even if we don't
// include the vertex at current index.
if (index1 >= l){
vector<int> newvec(arr1.begin(), arr1.end());
newvec.push_back(index1);
return (func(graph1, newvec, l - 1,
index1 - 1, sol1) or
func(graph1, arr1, l, index1 - 1, sol1));
}
// Now set of size l cannot be formed if we don't
// include the vertex at current index.
else{
arr1.push_back(index1);
return func(graph1, arr1, l - 1,
index1 - 1, sol1);
}
}
}
// Shows function to verify if the given set is
// independent or not
// arr --> set of size l (contains the
// index of included vertex)
bool check1(int graph1[][5], vector<int>&arr1, int n1){
// Verify if each vertex is connected to any other
// vertex in the set or not
for (int i = 0; i < n1; i++)
for (int j = i + 1; j < n1; j++)
if (graph1[arr1[i]][arr1[j]] == 1)
return false;
return true;
}
// Driver Code
int main(){
int graph1[][5] = {{1, 0, 1, 0, 0},{0, 1, 1, 0, 0},{1, 1, 1, 1, 1},{0, 0, 1, 1, 0},
{0, 0, 1, 0, 1}};
int l = 4;
vector<int> arr1; // Empty set
bool sol1[] = {false};
int n1 = sizeof(graph1) /
sizeof(graph1[0]);
func(graph1, arr1, l, n1 - 1, sol1);
if (sol1[0])
cout << "Yes" << endl;
else
cout << "No" << endl;
return 0;
}Output
Yes
Updated on: 24-Jul-2020
73 Views
Advertisements