Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Program to find the diameter, cycles and edges of a Wheel Graph in C++
In this problem, we are given a number that denotes the number of vertices of a Wheel Graph. Our task is to create a Program to find the diameter, cycles and edges of a Wheel Graph in C++.
Problem description − Here, we need to find the number of cycles, number of edges, and the diameter of Wheel Graph with n vertices.
First, let’s understand some basics about Wheel Graph −
A wheel graph is obtained from a cycle graph Cn-1 by adding a new vertex. That new vertex is called a Hub which is connected to all the vertices of Cn.
Example of a wheel graph with 7 vertices.
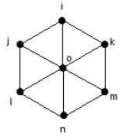
Diameter of wheel Graph is the number of edges that we need to cover to go from anyone vertices to others. For the above Wheel Graph, the diameter is 2
No. of Cycle of Wheel Graph is the total number of closed cycles that can be the given graph. For the above Wheel Graph, the no. of cycles is 31.
No. of Edge of Wheel Graph is the count of edges that connect all the vertices. For the above Wheel Graph, no of edges is 12.
Solution Approach
To solve the problem, we will be using the direct formula that is given in the graph theory to find the required values for a wheel graph.
The Formulas are,
Diameter of a Wheel Graph =
1, if vertices = 4, else 2.
No. of cycles of a Wheel Graph =
(No. of vertices )^2 - (3 * (No. of vertices -1) )
No. of edges of a wheel Graph =
2 * (No. of vertices - 1)
Program to illustrate the working of our solution,
Example
#include <iostream>
#include <math.h>
using namespace std;
void calcValuesWheelGraph(int V){
// Calculating the Diameter
if(V == 4){
cout<<"The Diameter of the Wheel Graph is 1 "<<endl;
}
else {
cout<<"The Diameter of the Wheel Graph is 2 "<<endl;
}
// Calculating the no. of cycles
cout<<"The number of cycles of the Wheel Graph is "<<(pow(V, 2) - (3 * (V-1)))<<endl;
// Calculating the no. of Edges
cout<<"The number of Edges of the Wheel Graph is "<<(2 * (V-1))<<endl;
}
int main(){
int V = 9;
calcValuesWheelGraph(V);
return 0;
}Output
The Diameter of the Wheel Graph is 2 The number of cycles of the Wheel Graph is 57 The number of Edges of the Wheel Graph is 16
245 Views
