
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program to Check Whether an Undirected Graph Contains a Eulerian Cycle
The Euler path is a path by which we visit every edge exactly once while using the same vertices multiple times. When the starting and ending vertex of the Euler path is the same node (i.e., if a path starts from node 'A' and ends on node 'A'), it is also known as the Eulerian cycle.
In this article, our task is to check if the Eulerian cycle exists in the given undirected graph or not.
Example of Eulerian Cycle
The figure below displays an undirected graph and its respective adjacency matrix. As we can see there exists an Eulerian cycle in the graph and its starting and ending nodes are the same i.e., 0.
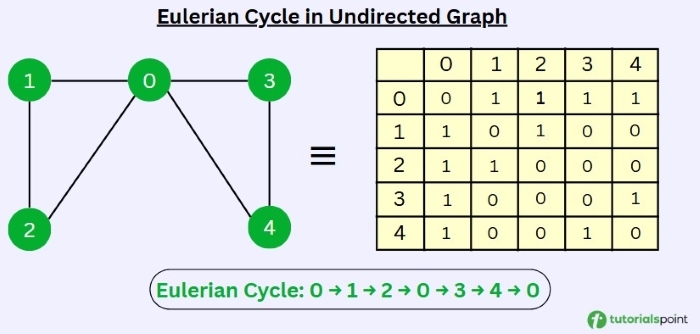
Conditions to Check Eulerian Cycle in Undirected Graph
The conditions for checking an undirected graph if there exists any Eulerian Cycle or not, are given below. If any of these conditions fails, the graph has no Eulerian path.
- The undirected graph should be a connected graph.
- The degree of each vertex of the graph should be even.
Steps to Check Eulerian Cycle in Undirected Graph
The steps given below are used to check if the given undirected graph has an Eulerian cycle or not:
- We defined the number of nodes and provided the adjacency matrix of the graph. After that, we check all the conditions required for the Eulerian cycle in the graph.
- The first condition is to check if the given graph is a connected graph. We have used the Depth-First Search(DFS) algorithm to mark the nodes as visited using the dfs() function.
- In the isCycle() function, we have defined a degree counter that keeps the count of degree of each vertex.
- Then we check the value stored in the degree. If degree of all the nodes is even, it returns true.
- If both conditions (connected graph and even degree of each vertex) are true, the function returns true which indicates an Eulerian cycle is present.
- If the given graph has an Eulerian cycle, then the Eulerian cycle is printed using the printCycle() function.
C++ Implementation of Checking Eulerian Cycle in Undirected Graph
The following code implements the above steps to check the undirected graph for the Eulerian cycle.
#include <iostream>
#include <vector>
#define NODE 5
using namespace std;
int graph[NODE][NODE] = {{0, 1, 1, 1, 1},
{1, 0, 1, 0, 0},
{1, 1, 0, 0, 0},
{1, 0, 0, 0, 1},
{1, 0, 0, 1, 0}};
// Function to implement DFS
void dfs(int u, bool visited[]) {
visited[u] = true;
for (int v = 0; v < NODE; v++) {
if (graph[u][v] && !visited[v])
dfs(v, visited);
}
}
// Function for checking if graph is connected or not
bool isConnected() {
bool visited[NODE] = {false};
int start = -1;
for (int i = 0; i < NODE; i++) {
for (int j = 0; j < NODE; j++) {
if (graph[i][j]) {
start = i;
break;
}
}
if (start != -1) break;
}
if (start == -1)
return true;
// Starting DFS from the found vertex
dfs(start, visited);
// Checking if all nodes are visited or not
for (int i = 0; i < NODE; i++) {
for (int j = 0; j < NODE; j++) {
if (graph[i][j] && !visited[i])
return false;
}
}
return true;
}
// Function for checking if graph has Eulerian cycle
bool isCycle() {
if (!isConnected())
return false;
for (int i = 0; i < NODE; i++) {
int degree = 0;
for (int j = 0; j < NODE; j++) {
if (graph[i][j])
degree++;
}
if (degree % 2 != 0)
return false; // Checking if the degree is even
}
return true;
}
vector<int> eulerCycle;
void printCycle(int u) {
for (int v = 0; v < NODE; v++) {
while (graph[u][v]) {
graph[u][v]--;
graph[v][u]--;
printCycle(v);
}
}
eulerCycle.push_back(u);
}
int main() {
if (isCycle()) {
cout << "The given undirected graph has an Eulerian Cycle.\n";
printCycle(0);
cout << "Eulerian Cycle: ";
int n = eulerCycle.size();
for (int i = n - 1; i >= 0; i--) {
cout << eulerCycle[i];
if (i) cout << " -> ";
}
cout << endl;
} else {
cout << "The given undirected graph does NOT have an Eulerian Cycle.\n";
}
return 0;
}
The output of the above code is as follows:
The undirected graph has an Eulerian Cycle. Eulerian Cycle: 0 -> 1 -> 2 -> 0 -> 3 -> 4 -> 0
Complexity to Check Eulerian Cycle in Undirected Graph
- Time Complexity: The time complexity for checking the Eulerian cycle in the undirected graph is O(v^2).
- Space Complexity: The space complexity for checking the Eulerian cycle in the undirected graph is O(v^2).

