
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Magnetism, Electromagnetism & Magnetic Materials
Magnetism
In the ancient times, people believed that the invisible forces of magnetism was purely a magical quantity. However, with the increasing scientific knowledge over the passing centuries, magnetism assumed a larger and larger role. Today the magnetism has attained a place of pride in electrical engineering. Without the magnetism, it is impossible to operated electrical devices like generators, motors, transformers, TV, radio, telephone etc. Therefore, electrical engineering is much dependent on magnetism.
Magnetic poles
A magnet has two poles viz. North Pole and South Pole. In order to determine the polarity of a magnet, suspend it at its centre, then the magnet will come to rest in north-south direction. Therefore, the end of magnetic pointing north of the earth is called North Pole of the magnet while the end pointing the south of earth is called South Pole of the magnet.

Some important points about magnetic poles −
The poles of a magnet cannot be separated, i.e. if a bar magnet is broken into two parts, each piece will contain N-pole at one end and S-pole at the other.
Magnetic poles have no physical reality.
The N-pole and S-pole of a magnet has equal strength.
Laws of Magnetic Forces
There are two laws states about the nature and magnitude of magnetic force between two magnetic poles −
Like magnetic poles repel each other while unlike magnetic poles attract each other, i.e. N-pole & N-pole or S-pole & S-pole repel each other while N-pole & S-pole attract each other.
The force acting between the two magnetic poles is directly proportional to the product of their pole strengths (m) and inversely proportional to the square of distance (r) between them.

Therefore, force between two magnetic poles is
$$\mathrm{F\:α\frac{m_{1}\:m_{2}}{r^{2}}}$$
$$\mathrm{\Rightarrow\:F\:=\:K\frac{m_{1}\:m_{2}}{r^{2}}}\:\:\:… (1)$$
Where, K is a proportionality constant that is given as,
$$\mathrm{K=\frac{1}{4\pi\:\mu_{o}\mu_{r}}}\:\:\:… (2)$$
Where,
μ0 is the absolute permeability of air / vacuum. Its value is 4π10-7 H/m,
μr is the relative permeability of surrounding medium, (for air, μr = 1).
Thus, from equations (1) and (2), we can write,
$$\mathrm{F=\frac{1}{4\pi\:\mu_{o}\mu_{r}}(\frac{m_{1}\:m_{2}}{r^{2}})}\:\:\:… (3)$$
The pole strength (m) is measured in Weber (Wb).
Magnetic Field and its Properties
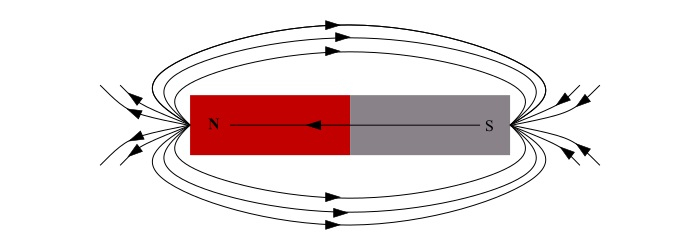
The field or space in which a magnetic pole experiences a force is known as magnetic field. The magnetic field of a magnet is represented by imaginary lines around it, which are known as magnetic field lines.
Properties of magnetic field lines
The magnetic field lines form a closed loop, i.e. they emerge from N-pole of the magnet, pass through the surrounding medium and enter the S-pole.
The tangent of a magnetic field line at a point on it, represents the direction of magnetic flux density (B) at that point.
Two magnetic field lines never intersect each other. If two magnetic field lines intersect at a point, there would be two directions of magnetic field at that point.
The magnetic field lines contract longitudinally and widen laterally. This explains that like poles repel each other while unlike poles attract.
Magnetic Flux
The magnetic flux is defined as the total number of magnetic field lines produced by a magnet. It is denoted by Phi (Φ) and given by,
$$\mathrm{Magnetic\:flux,Φ = m\:Weber(Wb)}\:\:\:… (4)$$
Magnetic Flux Density
The magnetic flux density is defined as the magnetic flux passing normally per unit area. It is denoted by B. It is a vector quantity having both magnitude and direction. Thus,
$$\mathrm{Magnetic\:flux\:density,B=\frac{Φ}{A}\:Wb⁄m^{2}\:or\:Tesla}\:\:\:…(5)$$
Magnetic Intensity
The force acting on a unit test N-pole placed at a point in the magnetic field, is termed as magnetic intensity or magnetic field strength or magnetising force. It is denoted by H.

Here,
$$\mathrm{Magnetic\:intensity\:at\:x,H=force\:on\:unit\:test\:N-pole\:placed\:at\:x}$$
$$\mathrm{\Rightarrow\:H=\frac{1}{4\pi\mu_{0}}(\frac{m×1}{r^{2}})=\frac{1}{4\pi\mu_{0}}(\frac{m}{r^{2}})}\:\:\:N⁄Wb \:\:\:…(6)$$
The magnetic intensity is a vector quantity, possessing both magnitude and direction.
Relation between B and H
The magnetic flux density (B) is directly proportional to magnetic intensity (H), in a given magnetic material, i.e.
$$\mathrm{B\:α\:H}$$
$$\mathrm{\Rightarrow\:B=\mu H=\mu_{0}\mu_{r}H}\:\:\:… (7)$$
Electromagnetism
When an electric current flows through a conductor (or coil), magnetic field is produced around the conductor (or coil). Therefore, the phenomenon of production of magnetic field due to electric current is called as electromagnetism.
Current through a straight wire
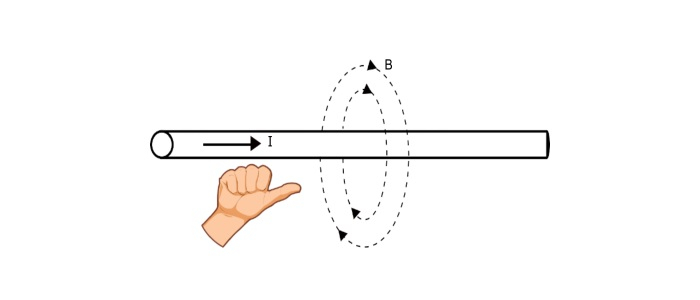
When electric current flows through a straight wire, magnetic field produces around the conductor. The magnetic field lines are in the form of concentric circles around the conductor. The direction of magnetic field lines around the conductor depends upon the direction of current through it and may be determined by using any one of following rules −
Right Hand Rule
Hold the conductor in the right hand, if the thumb is pointing in direction of current, then the curled fingers will point the direction of magnetic around the conductor (as shown in the figure).
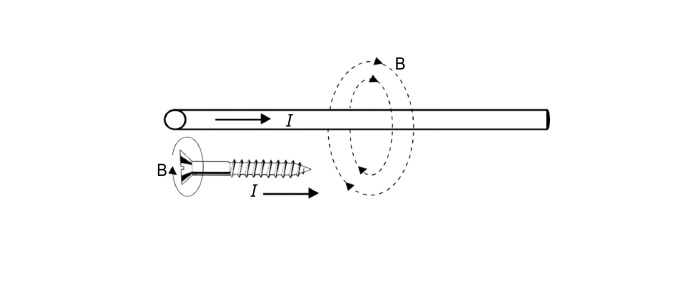
Cork Screw Rule
Hold the cork screw in the right hand and rotate it in such a way that it advances in the direction of current. Then the direction in which hand rotates will be the direction of magnetic field line around the conductor (see the figure).
Current carrying coil
Consider a coil consists of N turns wound around an iron core. When an electric current flows in the coil, a magnetic field produces around the coil. The one end the core becomes N-pole whereas another end S-pole depending upon the direction of the current in the coil. This arrangement is commonly known as electromagnet. The polarity of this electromagnet can be determined by using right hand rule for coil.
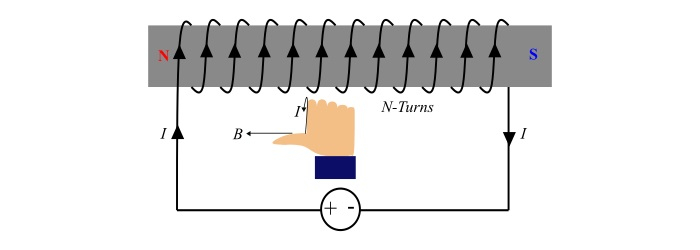
Right-hand rule for coil
Grasp the coil in the right hand in such a way that the curled fingers represents the direction of current, then the thumb stretched parallel to the axis of the coil will point towards the north-pole of the electromagnet.
Magnetising Force (H) of an Electromagnet
Consider a coil of N turns carrying a current of I amperes (as shown in the above figure). The magnetic flux (Φ) produced by the coil is directly proportional to the product of number of turns (N) of the coil and current (I). The quantity NI is known as magnetomotive force (m.m.f) and is measured in Ampere-Turns (AT).
$$\mathrm{mmf=NI\:\:\;AT}\:\:\:… (8)$$
Now, the magnetising force (H) of an electromagnet is defined as the mmf set up per unit length of the magnetic circuit, i.e.
$$\mathrm{Magnetising\:force,H=\frac{NI}{l}}\:\:\:AT/m…(9)$$
Magnetic Materials
A magnetic material is one that produces magnetic field. Generally, magnetic materials are classified into three categories as follows −
- Diamagnetic materials
- Paramagnetic materials
- Ferromagnetic materials
Diamagnetic Materials
The diamagnetic materials, sometimes called as non-magnetic materials are the materials that does not have any significant magnetism. In these materials, the resultant magnetic moment being zero. When a diamagnetic material is placed under the influence of an external magnetic field, the material produces a magnetic field that opposes the external magnetic field. For this reason, the diamagnetic material is repelled by the external magnetic field. Examples of diamagnetic materials are water, wood, organic compounds like petroleum and some plastics and some metals like copper, mercury, gold, silver, carbon etc.
Paramagnetic Materials
The paramagnetic materials are the materials that has a very little magnetic properties. In these materials, the atoms have some unpaired electrons and the magnetic moment of individual electrons cannot completely cancel out. Hence, the atoms have some magnetic moment that is aligned in random directions, so the paramagnetic material as a whole does not exhibit magnetism.
If a paramagnetic material is placed in an external magnetic field, the magnetic moments of individual atom are aligned with the external field. This causes the material to become magnetised. Hence, the magnetic field produced by the paramagnetic material is directed in the same direction as the external magnetic field. The paramagnetic materials exhibits magnetism only as long as they are under the influence of external magnetic field. If the external magnetic field is removed, the paramagnetic material loses its magnetism. The examples of paramagnetic materials are sodium, aluminium, lithium, magnesium, tungsten etc.
Ferromagnetic Materials
The ferromagnetic materials are those that can easily magnetised and they can retain their magnetism. In the ferromagnetic materials, the atoms have unpaired electrons, so each atom has a resultant magnetic moment. The magnetic moment of nearby atoms have a tendency to become aligned. These nearby atoms create different regions in the material that are called domains, where the magnetic moments of individual atom are aligned. However, the magnetic moments of different domains may still directed in different directions. When a ferromagnetic material is placed inside an external magnetic field, the different domains of the material align along the external magnetic field. Even, if the external magnetic field is removed, the ferromagnetic material retains its magnetism. The examples of ferromagnetic materials are most metals like iron, nickel, cobalt and some alloys of metals etc.

