Linear Programming

Introduction

Linear programming or linear optimization is a unique tool used to obtain the optimum (maximum or minimum) value of a mathematical model. It is abbreviated as LP and it is also known as mathematical optimization. In this tutorial, we will learn about linear programming, different methods to solve linear programming problems, and its various types.

Linear Programming

• Linear programming is defined as the mathematical optimization process in which the maxima and minima of the process outcomes are evaluated within specific constraints.

• In other words, it is a technique to optimize the linear objective function.

• The linear programming problem (LPP) has three parts: objective function, linear equality or constraints, and non-negative restrictions.

• The objective function is a linear function of process variables, which need to be optimized.

• The constraints are the boundary limit or restrictions of the process variables. The standard form of the linear programming problem can be expressed as

Objective function − $\mathrm{g(x_{1},x_{2}\:=\:q_{1}x_{1}\:+\:q_{2}x_{2})}$

Constraints − $\mathrm{m_{11}x_{1}\:m_{12}x_{2}\:\leq\:s_{1}}$

$\mathrm{m_{21}x_{1}\:+\:m_{22}x_{2}\:\leq\:s_{2}}$

Non-negative restrictions − $\mathrm{x_{1}\:\geq\:0,\:x_{2}\:\geq\:0}$

Methods to Solve LPP

There are mainly two types of methods to solve LPP such as

• Graphical method

• Simplex method

Let’s discuss each type of method in detail.

Graphical

• Construct the LPP in its standard form.

• Draw a graph in a cartesian plane and draw the constraint lines

• Determine the valid side of each constraint line.

• Evaluate the feasible solution region and obtain the corner points

• Put the corner point in the objective function to get the desired outcome

Simplex

• Step 1 − The first step involved adding the slack variable to the objective function to convert the inequalities to equation form.

• Step 2 − Construct an initial simplex table and write the objective function as the bottom row.

• Step 3 − Identify the most negative entry of the column and marked as a pivot column.

• Step 4 − Find the quotient by dividing the entries in the rightmost column by the entries of the pivot column. The row containing the smallest quotient is marked as the pivot row. Mark the pivot element that is the intersection of pivot row and column

• Step 5 − Make all the entries of the pivot column to zero by performing elementary operations.

• Step 6 − Stop the step if we get non-negative integers in the bottom row; otherwise, repeat the step starting from step 4.

Types of LPP

There are the following types of LPP that are discussed below.

Nutrition

This type of LPP is used to optimize the diet plan. In other words, the optimization of the intake of food with a minimum budget is the objective of this LPP.

• Objective function − The budget for diet

• Constraints − The minimum/maximum amount of a specific diet, such as sugar and cholesterol in the food.

Production/Cost

This type of LPP involves the optimization of the net profit or production rate of a manufacturing unit.

• Objective function − Production rate or net profit

• Constraints − Production cost, Employee cost, packaging cost, etc.

Transportation

This LPP aims to provide efficient transportation with a minimum cost

• Objective function − The transportation cost

• Constraints − Supply or demand of the goods

Solved examples

Example 1

One type of bread requires 250 g of flour and 20 g of fat. Another type of bread requires 150 g of flour and 30 g of fat. Find the maximum number of bread that can be produced from 3 kg of flour and 0.6 kg of fat.

Solution −

Step 1 − Let’s tabulate the given data for the better understanding

	Weight of floor (g)	Weight of fat (g)
First type of bread (x)	250	20
Second type of bread (y)	150	30
Availability	3000	600

Step 2 − We have to formulate the objective function and constraints from the given data.

Objective function $\mathrm{g\:=\:x\:+\:y}$

Constraints $\mathrm{250x\:+\:150y\:\leq\:3000\:or\:5x\:+\:3y\:\leq\:60}$

$\mathrm{20x\:+\:30y\:\leq\:600\:or\:2x\:+\:3y\:\:leq\:60}$

Non-negative restrictions $\mathrm{x_{1}\:\geq\:0\:,\:x_{2}\:\geq\:0}$

Step 3 − Draw the straight lines, i.e., $\mathrm{5x\:+\:3y\:=\:60}$ and $\mathrm{2x\:+\:3y\:=\:60}$ on the cartesian plane.

The constraint line $\mathrm{5x\:+\:3y\:=\:60}$ meets the coordinate axis at (12, 0) and (0, 20). Hence, any point that lies below the region of the straight line satisfies $\mathrm{5x\:+\:3y\:\leq\:60}$

Similarly, the line $\mathrm{2x\:+\:3y\:=\:60}$ meets the coordinate axis at (30, 0) and (0, 20). Hence, any point that lies below the straight line region satisfies $\mathrm{2x\:+\:3y\:\leq\:60}$. The corner points and the corresponding values of the objective function are provided below

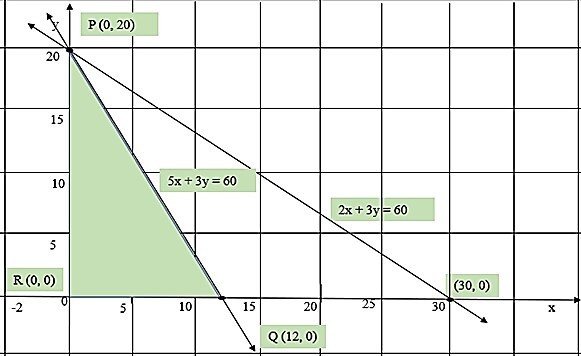
Corner points	$\mathrm{g(x,y)\:=\:x\:+\:y}$
P (0, 20)	20
Q (12. 0)	12
R (0,0)	0

∴The maximum number of bread that can be formed is 20 and the optimum solution is (0,20).

Example 2

Solve the LPP using the simplex method.

Maximize $\mathrm{f(x,y)\:=\:7x\:+\:5y}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:x\:+\:2y\:\leq\:6}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:4x\:+\:3y\:\leq\:12}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:x,y\:\geq\:0}$

Solution

Add slack variables to the above inequalities to convert them into equations

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:7x\:+\:5y\:=\:p}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:x\:+\:2y\:+\:q\:=\:6}$

$\mathrm{\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:4x\:+\:3y\:+\:r\:=\:12}$

The simplex table is formulated as below.

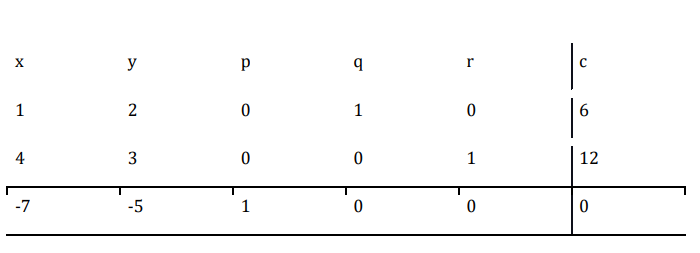
Here, the first column is the pivot column as it contains the highest negative number $$

Now $\mathrm{\frac{6}{1}\:=\:6\:and\:\frac{12}{4}\:=\:3}$

Since 3 is found to be the smaller quotient, the second row is the pivot row answer 4 is the pivot element.

Now, using the elementary operations

$\mathrm{R_{2}\:\rightarrow\:\frac{R_{2}}{4}}$

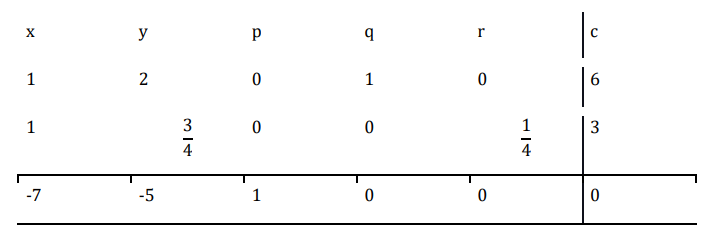
Now perform $\mathrm{R_{1}\:\rightarrow\:R_{1}\:-\:R_{2}}$

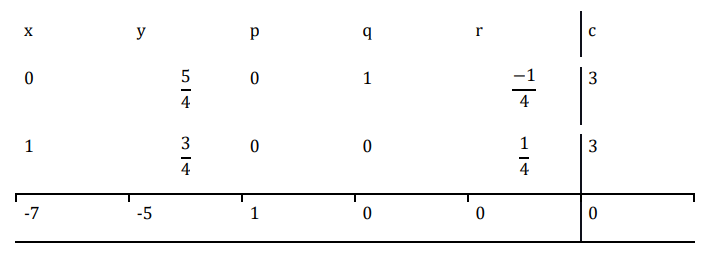
Now perform $\mathrm{R_{3}\:\rightarrow\:7R_{2}\:+\:R_{3}}$

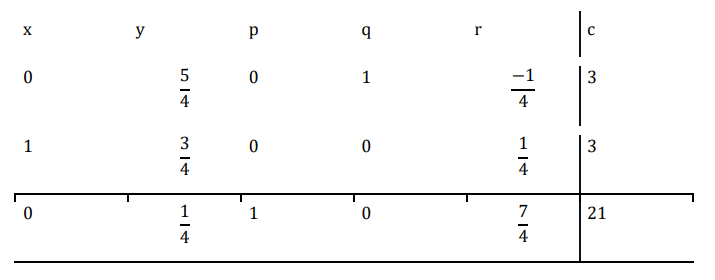
∴The maximum value of the function is 21 and the optimum solution is (3,0).

Conclusion

The present tutorial gives a brief introduction about the linear programming. In addition, various types and methods to solve LPPs have been briefly described. Moreover, some solved examples have been provided for better clarity of this concept. In conclusion, it may be useful for understanding the basic concept of linear programming problems.

FAQs

1. What do you mean by the feasible region in the graphical method?

The feasible region is the area bounded by the coordinates, which satisfy the given constraints.

2. What are the applications of LP?

LP has many applications, including production scheduling, inventory policies, technology, construction of warehouses, etc.

3. Define the objective function?

An objective function is a real-valued function, which is to be either maximized or minimized

4. What is the limitation of the graphical method?

The graphical method becomes complex with an increase of variables and constraints. It is more suitable for the objective functions to become complex with increased variables and constraints.

5. Can a LPP have multiple solutions?

Yes. A LPP can have multiple solutions.