Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Inverting and Non-Inverting Operational Amplifiers
An operational amplifier is a three-terminal device consisting of two high impedance input terminals, one is called the inverting input denoted by a negative sign and the other is the non-inverting input denoted with a positive sign. The third terminal is the output of the Op-Amp.
Inverting Operational Amplifier
In the inverting operational amplifier circuit, the signal is applied at the inverting input and the non-inverting input is connected to the ground. In this type of amplifier, the output is 180⁰ out of phase to the input, i.e. when positive signal is applied to circuit, the output of the circuit will be negative. By assuming the Op-Amp is ideal, then the concept of virtual short can be applied at the input terminals of the Op-Amp. So that voltage at the inverting terminal is equal to the voltage at non-inverting terminal.
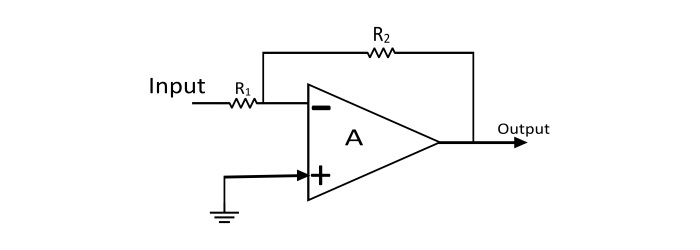
Applying KCL at inverting node of Op-Amp
$$\mathrm{\frac{0-V_{in}}{R_{1}}+\frac{0-V_{out}}{R_{2}}=0}$$
$$\mathrm{Voltage\:Gain(A_{v})=\frac{V_{out}}{V_{in}}=-\frac{R_{2}}{R_{1}}}$$
Non-Inverting Operational Amplifier
When the signal is applied at the non-inverting input, the resulting circuit is known as Non-Inverting Op-Amp. In this amplifier the output is exactly in phase with the input i.e. when a positive voltage is applied to the circuit, the output will also be positive. By assuming the Op-Amp is ideal, then concept of virtual short can be applied i.e. the voltage at the inverting and non-inverting terminal is equal.
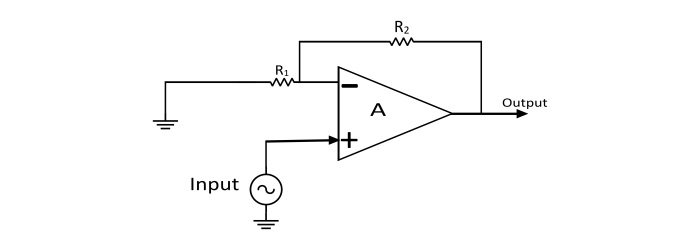
Applying KCL at the inverting node
$$\mathrm{\frac{V_{in}-V_{out}}{R_{2}}+\frac{V_{0}-0}{R_{1}}=0}$$
$$\mathrm{Voltage\:Gain(A_{v})=\frac{V_{out}}{V_{in}}=1+\frac{R_{2}}{R_{1}}}$$
Difference between Inverting and Non-Inverting Op-Amps
| Inverting Op-Amp | Non-Inverting Op-Amp |
|---|---|
| The type of feedback used is voltage shunt. | The type of feedback used is voltage series. |
| The input and output voltages of this amplifier are 180⁰ out of phase. | The input and output voltages are in phase. |
| $$\mathrm{Voltage\:Gain(A_{v})=\frac{V_{out}}{V_{in}}=-\frac{R_{2}}{R_{1}}}$$ | $$\mathrm{Voltage\:Gain(A_{v})=\frac{V_{out}}{V_{in}}=1+\frac{R_{2}}{R_{1}}}$$ |
| The input impedance is R1. | The input impedance is very high. |
46K+ Views
To Continue Learning Please Login