Interval Heaps in Data Structure

Here we will see what is the interval heaps. The interval heaps are complete binary tree, in which, each node except possibly the last one contains two elements. Let the priorities of two elements in node P are ‘a’ and ‘b’. Here we are considering a ≤ b. We say that the node P represents the closed interval [a, b]. Here a is the left endpoint of the interval of P, and b is the right endpoint. The [c, d] is contained in the interval [a, b] if and only if a ≤ c ≤ d ≤ b. In an interval heap, the intervals represented by the left and right children of each node P are contained in the interval represented by P. When the last node is containing a single element with priority c, then a ≤ c ≤ b. Here [a, b] is interval of the parent of the last node.

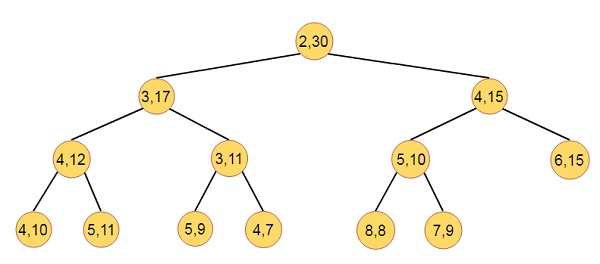
This is consisting of min and max heaps. The max and min heaps.

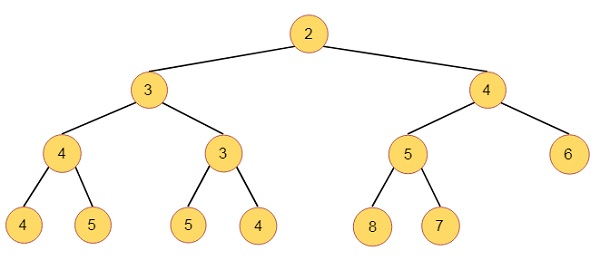
This is Min Heap

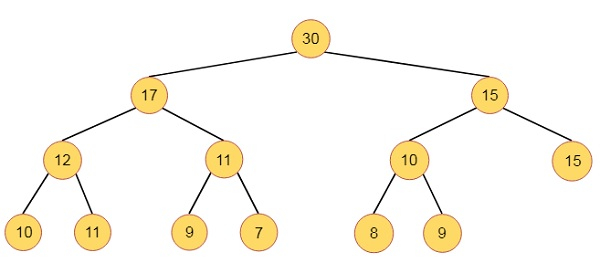
This is Max Heap