How to Read PACF Graph for Time Series?

Time series data analysis can be applied to a range of fields, including finance, economics, and marketing. The autocorrelation function (ACF) and partial autocorrelation function (PACF) are extensively used in time series data analysis. A time series correlation between the observations is assessed using PACF plots. Finding the important lag values that enable estimating the series' future values is useful. Even yet, if you are unfamiliar with the PACF graph, it could be challenging to read. In this blog article, we'll help you through each step of comprehending a PACF graph for time series analysis.

What is PACF?

Partial Autocorrelation Function is referred to as PACF. With the influence of the intermediate lags being controlled, it is a statistical technique used in time series analysis to assess the direct link between an observation at a given lag and its preceding delays.

In other words, the PACF subtracts the impact of the further delays between two-time series to assess the correlation between their values at a certain lag. On the other hand, the autocorrelation function (ACF) examines the correlation between the values of two-time series at a certain lag without accounting for the intermediate delays. When examining autoregressive (AR) models in time series analysis, the PACF is a helpful tool. The sequence and number of delays that should be included in the AR model can be decided using the PACF.

PACF Graph

The partial autocorrelation values for various lag settings for a time series are shown on a PACF graph. The PACF graph facilitates the identification of the significant lag values for forecasting the future values of the series. In other words, the size of the significant delays in a PACF graph determines where to position the AR (Autoregressive) model for the time series.

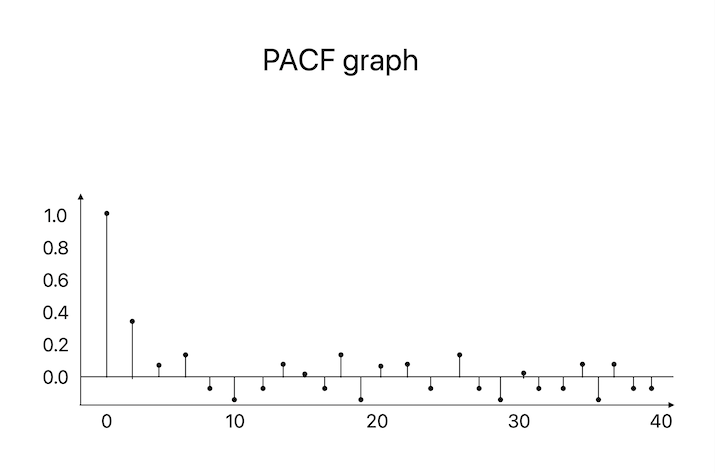
Let's look at how to interpret a PACF graph now that we've covered the fundamentals of PACF and PACF graphs.

Step 1: Determine the Range of Lag Values

Establishing the range of lag values is the first step in understanding a PACF graph. The distance in time between two observations in a time series is known as the lag value. For instance, the lag number will be one month if you are studying monthly sales data.

Look at the PACF graph's x-axis to find the range of lag values. The partial autocorrelation values are represented on the y-axis while the lag values are represented on the x-axis. The typical range of lag values, where n is the length of the time series, is 0 to n-1.

Step 2: Identify the Significance Level

Finding the level of relevance is the next stage. The partial autocorrelation values are taken into consideration to be significant when they reach the significance level. In the PACF graph, a horizontal line is typically used to indicate it.

The sample size and level of confidence both influence the significance threshold. Any partial autocorrelation value greater than the 95% significance threshold is deemed significant when using a 95% confidence level, which is the standard.

Step 3: Interpret the PACF Graph

The PACF graph can be understood once the significance level and the range of lag values have been established. The steps to understanding a PACF graph are as follows −

Step 3.1: Identify the Significant Lags

Finding the significant delays is the first step. Keep an eye out for partial autocorrelation values that are significant. These delays are noteworthy and show a direct correlation between the results at various lags.

Step 3.2: Determine the Order of the AR Model

The order of the AR (Autoregressive) model for the time series is determined in part by the substantial delays in a PACF graph. The number of significant lag values determines the AR model's order. For instance, the AR model's order will be 2 if lag values 1 and 2 are substantial.

Step 3.3: Check for Cut-off

The cut-off is a crucial factor to take into account when evaluating a PACF graph. After the large delays, there is a progressive decline in the partial autocorrelation values known as a cut-off. The cut-off implies that the only lags that directly relate to the values at distinct lags are the important delays. If there is no cut-off, the AR model can also need to take into account additional lags that have a direct link with the values at distinct delays.

Step 3.4: Interpret Non-Significant Lags

A non-significant lag on the PACF graph, on the other hand, means that there is no direct correlation between the values at that lag. With the AR model, these delays can be disregarded.

A partial autocorrelation value that is negative and substantial could occasionally exist. This shows that there is a bad correlation between the results at various delays. While choosing the order of the AR model in such circumstances, the negative correlation should be taken into consideration.

Conclusion

In conclusion, PACF graphs are effective time series analysis tools, particularly when looking at AR models. They assist in locating the major lag values that are closely related to the values at various delays. Finding the range of lag values, the significance level, the significant lags, the order of the AR model, the cut-off, and the non-significant delays are all necessary for interpreting a PACF graph.

It might be a little intimidating to read PACF graphs if you are new to time series analysis. Yet with time and effort, you can master reading PACF graphs and applying them to time series data analysis.