Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to create normal quantile-quantile plot for a logarithmic model in R?
How to create normal quantile-quantile plot for a logarithmic model in R?
A logarithmic model is the type of model in which we take the log of the dependent variable and then create the linear model in R. If we want to create the normal quantile-quantile plot for a logarithmic model then plot function can be used with the model object name and which = 2 argument must be introduced to get the desired plot.
Example1
> x1<-rnorm(100,5,1) > x1
Output
[1] 4.735737 3.631521 5.522580 5.538314 5.580952 4.341072 4.736899 2.455681 [9] 4.042295 5.534034 4.717607 6.146558 4.466849 5.444437 5.390151 4.491595 [17] 4.227620 4.223362 5.452378 5.690660 5.321716 5.269895 2.810042 4.295378 [25] 5.767740 3.939896 6.213647 4.608487 5.094318 4.621997 4.801568 6.329819 [33] 4.339835 3.172058 6.031193 5.123346 5.673534 5.668435 5.754537 4.164556 [41] 6.630504 5.209786 7.171595 4.713524 4.382267 5.204943 5.895252 4.413933 [49] 5.491437 3.806081 6.283097 4.892824 3.698107 4.758340 3.612643 4.670258 [57] 5.376201 6.440996 3.589660 4.990421 6.649452 5.549918 4.224869 5.604002 [65] 4.667142 5.522634 4.820425 4.278682 4.611169 3.801012 4.774964 4.678297 [73] 4.087518 5.705981 5.812739 4.585449 3.328274 3.626282 4.637604 3.707011 [81] 5.661713 4.671823 6.033384 3.553500 3.945178 3.065177 4.260533 5.226990 [89] 4.852304 4.995663 5.229401 6.588605 5.375225 6.089018 4.199044 6.520236 [97] 5.569930 7.400434 6.291279 4.593149
Example
> y1<-rpois(100,10) > y1
Output
[1] 10 13 10 11 12 10 7 10 15 6 6 7 8 11 14 16 7 11 14 11 7 7 9 7 7 [26] 13 8 11 12 14 13 8 12 6 9 15 10 8 9 12 11 12 9 10 12 15 11 14 12 13 [51] 8 8 19 10 7 9 9 16 13 8 8 6 9 11 11 18 11 12 12 15 7 12 10 8 10 [76] 10 14 11 5 9 6 11 13 8 9 10 6 6 13 12 14 12 9 11 11 8 9 12 13 5
> Model1<-lm(log(y1)~x1) > summary(Model1)
Call:
lm(formula = log(y1) ~ x1)
Residuals:
Min 1Q Median 3Q Max -0.69827 -0.19657 0.01667 0.19465 0.61978
Coefficients:
Estimate Std. Error t value Pr(>|t|) (Intercept) 2.39474 0.15197 15.758 <2e-16 *** x1 -0.01895 0.03011 -0.629 0.531 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.2895 on 98 degrees of freedom
Multiple R-squared: 0.004024, Adjusted R-squared: -0.006139
F-statistic: 0.3959 on 1 and 98 DF, p-value: 0.5307
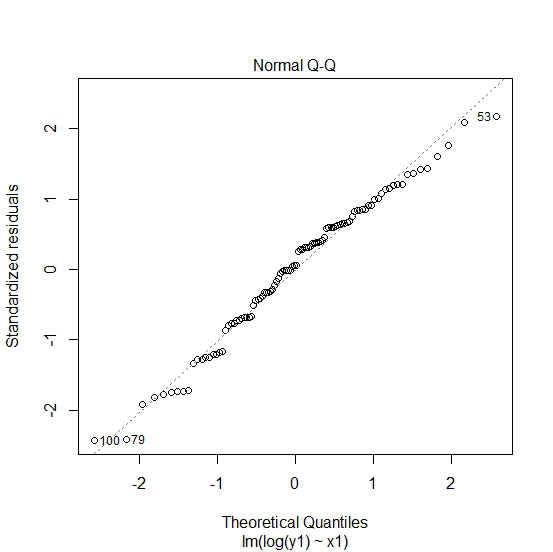
Creating the normal quantile-quantile plot:
> plot(Model1,which=2)
Output:
Example2
> x2<-rpois(100,5) > x2
Output
[1] 3 7 13 4 6 2 4 3 2 7 4 6 3 11 6 5 5 6 6 2 3 7 8 3 1 [26] 8 5 2 2 3 7 6 7 4 7 2 4 3 4 2 5 2 4 5 3 5 8 5 3 3 [51] 6 2 8 3 4 7 3 5 5 3 7 4 7 6 6 6 10 5 4 3 5 7 3 3 5 [76] 4 9 3 7 8 7 2 6 5 7 5 6 6 5 3 9 9 5 4 2 5 5 5 6 4
Example2
> y2<-rpois(100,12) > y2
Output
[1] 16 8 10 12 11 11 6 15 3 12 8 11 9 12 8 18 7 13 10 17 15 17 15 10 11 [26] 12 16 12 17 13 11 17 16 14 15 10 12 9 10 14 9 6 12 17 14 9 10 9 13 5 [51] 16 12 17 11 10 12 13 18 12 14 19 9 14 11 14 12 6 7 6 16 9 10 11 15 10 [76] 11 8 13 7 16 19 18 8 13 15 11 7 12 7 9 9 14 14 13 15 10 14 11 13 11
> Model2<-lm(log(y2)~x2) > summary(Model2)
Call:
lm(formula = log(y2) ~ x2)
Residuals:
Min 1Q Median 3Q Max -1.31858 -0.17210 0.04939 0.21912 0.50892
Coefficients:
Estimate Std. Error t value Pr(>|t|) (Intercept) 2.409861 0.081191 29.681 <2e-16 *** x2 0.003665 0.014863 0.247 0.806 --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.327 on 98 degrees of freedom
Multiple R-squared: 0.00062, Adjusted R-squared: -0.009578
F-statistic: 0.0608 on 1 and 98 DF, p-value: 0.8057
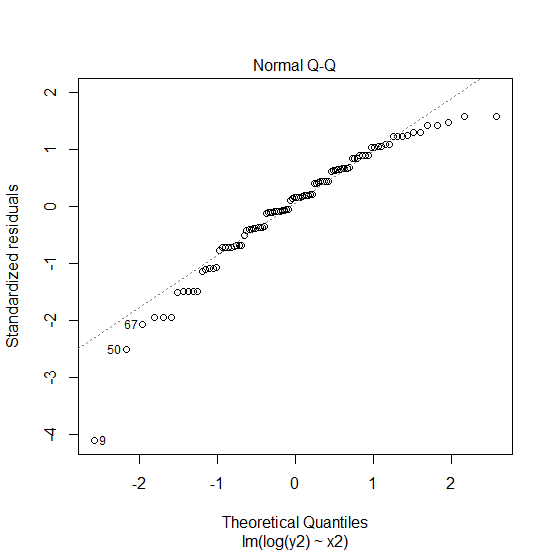
Creating the normal quantile-quantile plot:
> plot(Model2,which=2)
Output:
146 Views
