Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to convert FA to Right Linear Regular Grammar?
A grammar with at most one variable at the right side of production is called linear grammar.
Example 1
S→aSb/ε
Example 2
S→Ab
A→aAb
A→ε
Right Linear Grammar
A grammar is right linear grammar where all the non terminals in the right hand sides are at the right end.
For example,
S->aS/ε
Algorithm for conversion
The algorithm to convert the finite automata (FA) to the right linear grammar is as follows −
Step 1 − Begin the process from the start state.
Step 2 − Repeat the process for each state.
Step 3 − Write the production as the output followed by the state on which the transition is going.
Step 4 − And at last, add € (epsilon) to end the derivation.
Example 1
Let’s consider a Finite automaton (FA) as given below −
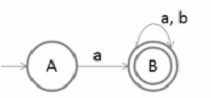
Pick the start state A and output is on symbol ‘a’ going to state B
A→aB
Now we will pick state B and then we will go on each output
i.e B→aB
B→bB
B→ε
Therefore,
Final right linear grammar is as follows −
A→aB
B→aB/bB/ε
Example 2
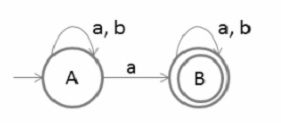
Start with state A which is an initial state the output on symbol ‘a’ goes to A and B and the output on symbol ‘b’ goes to A. Now the production rule of right linear grammar is −
A→aA/bA/aB
Now pick state B and then go on each output the right linear grammar is −
B→aB/bB/ε
The final right linear grammar for the given finite automata is −
A→aA/bA/aB
B→aB/bB/ε
5K+ Views
