How can SciPy be used to calculate the eigen values and eigen vectors of a matrix in Python?

Eigen vectors and Eigen values find their uses in many situations. The word ‘Eigen’ in German means ‘own’ or ‘typical’. An Eigen vector is also known as a ‘characteristic vector’. Suppose we need to perform some transformation on a dataset but the given condition is that the direction of data in the dataset shouldn’t change. This is when Eigen vectors and Eigen values can be used.

Given a square matrix (a matrix where the number of rows is equal to the number of columns), an Eigen value and an Eigen vector fulfil the below equation.

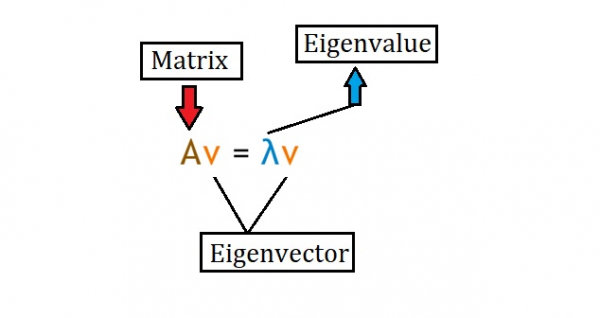
Eigen vectors are computed after finding the Eigen values.

Note − Eigen values work well with dimensions 3 or greater as well.

Instead of manually perfroming these mathematical computations, SciPy provides a function in the library called ‘eig’ which helps compute the Eigenvalue and the Eigenvector.

Syntax of ‘eig’ function

scipy.linalg.eig(matrix)

Let us see how the ‘eig’ function can be used −

Example

 Live Demo

from scipy import linalg
import numpy as np
my_arr = np.array([[5,7],[11,3]])
eg_val, eg_vect = linalg.eig(my_arr)
print("The Eigenvalues are :")
print(eg_val)
print("The Eigenvectors are :")
print(eg_vect)

Output

The Eigenvalues are :
[12.83176087+0.j -4.83176087+0.j]
The Eigenvectors are :
[[ 0.66640536 -0.57999285]
[ 0.74558963 0.81462157]]

Explanation

• The required libraries are imported.
• A matrix is defined with certain values in it, using the Numpy library.
• The matrix is passed as a parameter to the ‘eig’ function that computes the eigenvalues and the eigenvectors of the matrix.
• These computed data is stored in two different variables.
• This output is displayed on the console.