Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How can discrete Fourier transform be performed in SciPy Python?
Discrete Fourier Transform, or DFT is a mathematical technique that helps in the conversion of spatial data into frequency data.
Fast Fourier Transformation, or FTT is an algorithm that has been designed to compute the Discrete Fourier Transformation of spatial data.
The spatial data is usually in the form of a multidimensional array. Frequency data refers to data that contains information about the number of signals or wavelengths in a specific period of time.
Let us see how this DFT can be achieved using the ‘SciPy’ library.
The graph is created using the matplotlib library and data is generated using the Numpy library −
Example
From matplotlib import pyplot as plt
import numpy as np
my_freq = 6
freq_samp = 70
time_val = np.linspace(0, 3, 3 * freq_samp, endpoint = False )
amp_val = np.sin(my_freq * 3 * np.pi * time_val)
figure, axis = plt.subplots()
axis.plot(time_val, amp_val)
axis.set_xlabel ('Time (in seconds)')
axis.set_ylabel ('Amplitude of signal')
plt.show()
from scipy import fftpack
A = fftpack.fft(amp_val)
frequency = fftpack.fftfreq(len(amp_val)) * freq_samp
figure, axis = plt.subplots()
axis.stem(frequency, np.abs(A))
axis.set_xlabel('Frequency in Hz')
axis.set_ylabel('Frequency Spectrum Magnitude')
axis.set_xlim(-freq_samp / 2, freq_samp/ 2)
axis.set_ylim(-7, 125)
plt.show()Output
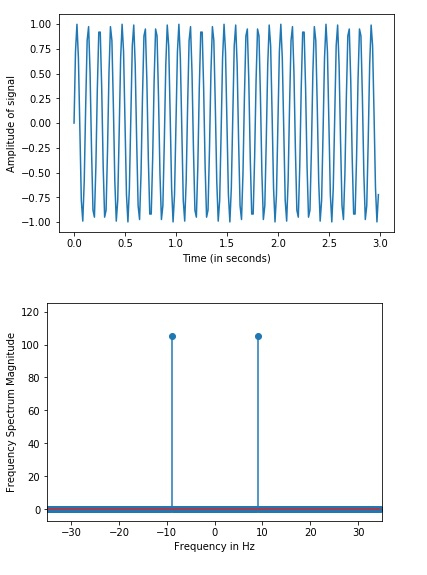
Explanation
- The required packages are imported.
- The data is generated with the help of Numpy library.
- This data is plotted as a sine wave on the console with the help of matplotlib library.
- Next, the ‘fftpack’ package is used to find the fast Fourier transform of the data generated.
- This data is again plotted on the graph.
Updated on: 10-Dec-2020
317 Views
Advertisements