Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Full Wave Rectifier
Full Wave Rectifier is a diode circuit which is used to transform the complete cycle of Alternating Voltage (AC Supply) to Direct Voltage (DC Supply).
In full wave rectification, current flows through the load in the same direction for the complete cycle of input AC Supply.
Types of Full Wave Rectifiers
- Centre Tap Full Wave Rectifier
- Full Wave Bridge Rectifier
Centre Tap Full Wave Rectifier
The circuit of centre tap full wave rectifier consists of following main components −
- Two Diodes
- A centre-tapped transformer
- A load resistance
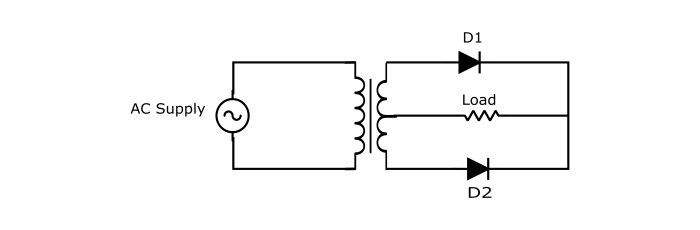
Working of Centre – Tap FWR Circuit
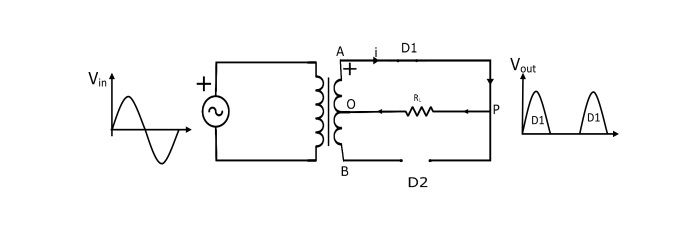
Positive Half Cycle
During the positive half cycle of input AC voltage, the end A of secondary winding becomes positive and the end B negative. This makes the diode D1 forward biased (acts as closed switch) and diode D2 reverse biased (acts as open switch). Therefore, current flows through the load (RL) from P to O.
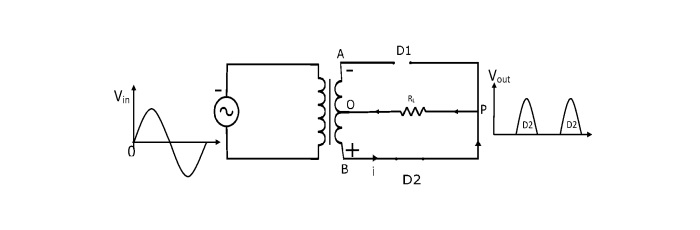
Negative Half Cycle
During the negative half cycle of input AC supply, the end B of secondary winding becomes positive and the end A negative. This makes the diode D2 forward biased (acts like closed switch) and the diode D1 reverse biased (acts as open switch). Therefore, the current will flow from B to O through diode D2, load RL and lower half of the secondary winding.
Note that the current through the load is in the same direction for both half cycles of input AC supply. Hence DC output is obtained across the load.
Output Frequency of Centre – Tap FWR
The output frequency is twice the input frequency. Since the input supply is sine wave that repeats every 2π radians. The output of FWR is pulsating DC that repeats the same pattern as input AC twice every 2π radians.
$$\mathrm{f_{out}=2f_{in}}$$
Disadvantages of Centre – Tap FWR
- The diodes must have peak inverse voltage.
- It is difficult to locate centre tap on secondary winding.
Full Wave Bridge Rectifier
The full wave bridge rectifier eliminates the need of centre tapped transformer. It contains four diodes connected to form bridge.
Circuit Diagram of Bridge FWR
The circuit of full wave bridge rectifier consists of following main components −
- Four Diodes
- A step down transformer
- A load resistance
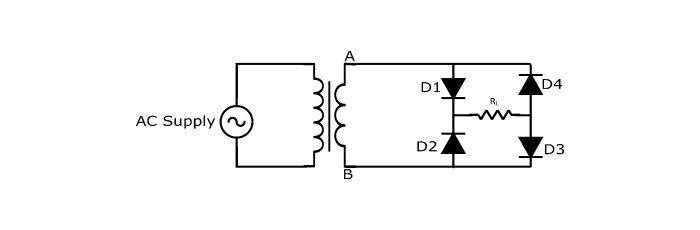
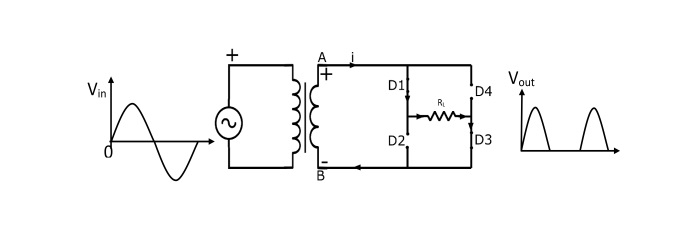
Working of Bridge FWR
Positive Half Cycle
During positive half cycle, the end A of secondary winding becomes positive and the end B negative. This makes diodes D1 and D3 forward biased (acts like closed switch) and diodes D2 and D4 reverse biased (acts like open switch). The current flows from A to B through diode D1, load RL and diode D3.
Negative Half Cycle
During Negative half cycle, the end A of secondary winding becomes negative and the end B positive. This makes diodes D1 and D3 reverse biased (acts like open switch) and diodes D2 and D4 forward biased (acts like closed switch). The current flows from B to A through diode D2, load RL and diode D4.
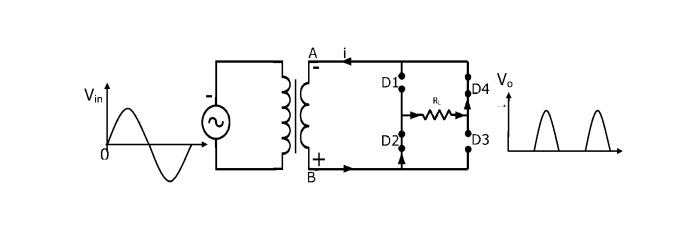
Therefore, the current flows through load RL in the same direction for both the cycles of input AC supply. Hence, DC output is obtained across the load.
Advantages of Bridge FWR
The output is twice that of the centre tap full wave rectifier for the same secondary voltage.
No need of centre tapped transformer.
For same DC output, PIV of full wave bridge rectifier is half that of Centre-Tap FWR.
Disadvantages of Bridge FWR
It requires four diodes.
During each half cycle of AC input, the two diodes that conduct are in series which causes voltage drop in internal resistance of diodes.
Full Wave Rectifier Waveform
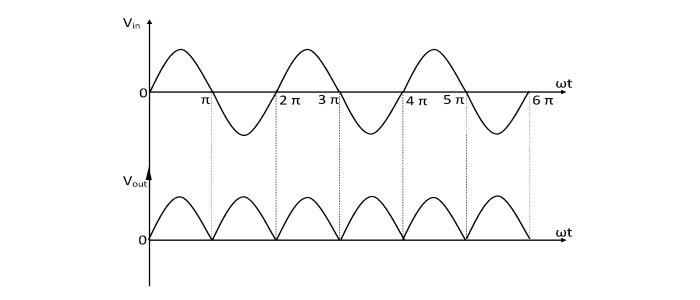
Full Wave Rectifier Formula
Efficiency of FWR
The efficiency of FWR is defined as the ration output DC power to the input AC power.
$$\mathrm{\eta=\frac{P_{dc}}{P_{ac}}}$$
The maximum efficiency of Full wave rectifier is 81.2%.
Peak Inverse Voltage of FWR
“The PIV is the maximum voltage that a diode can withstand without destruction when it is reverse biased”
For the centre – tap full wave rectifier, the PIV is twice of the maximum secondary winding voltage.
$$\mathrm{PIV=2V_{m}}$$
For Bridge FWR, the PIV of each diode is equal to the maximum secondary voltage.
$$\mathrm{PIV=V_{m}}$$
RMS Value of Load Current of FWR
$$\mathrm{I_{RMS}=\frac{I_{m}}{\sqrt{2}}}$$
Average Value of Load Current of FWR
$$\mathrm{I_{RMS}=\frac{2I_{m}}{\pi}}$$
DC Output Voltage of FWR
$$\mathrm{V_{dc}=V_{dc}R_{L}=V_{avg}R_{L}}$$
Form Factor of FWR
$$\mathrm {{Form\:Factor}=\frac{RMS \:Value}{Avg.Value}=\frac{V_{rms}}{V_{avg}}}$$
For FWR the form factor equals to 1.11
Ripple Factor of FWR
Ripple Factor gives the information about how a FWR can transform input AC voltage to output DC voltage. It is given by
$$\mathrm{Ripple\:Factor=\sqrt{(Form\:Factor)^2}-1}$$
The ripple factor for full wave rectifier is 0.482.
Numerical Example #1
In a centre tapped full wave rectifier, the internal resistance of each diode is . The transformer secondary RMS voltage from centre tap to each end of secondary is 60 V and load resistance is . Find −
- The average load current
- RMS value of load current
- DC output voltage
- Peak Inverse Voltage
Solution
RMS voltage across half secondary winding,Vrms=60V
Maximum voltage across half secondary winding,$V_{m}=60×\sqrt{2}=84.84 V$
$$\mathrm{(∵ V_{m}=𝑉V_{rms}×√2 )}$$
$$\mathrm{I_{m}=\frac{V_{m}}{R_{d}+R_{L}}=\frac{84.84}{(10+870)}=96.41 mA}$$
(a) The average load current
$$\mathrm{I_{avg}=\frac{2l_{m}}{\pi}=\frac{2×96.41}{\pi}=61.41 mA}$$
(b) The RMS value of load current
$$\mathrm{I_{rms}=\frac{l_{m}}{\sqrt{2}}=\frac{96.41}{\sqrt{2}}=68.18 mA}$$
(c) DC output voltage
$$\mathrm{V_{dc}=I_{avg}R_{L}=61.41×870=53.43 V}$$
(d) Peak Inverse Voltage
$$\mathrm{PIV=2V_{m}=2×84.84=169.68 V}$$
Numerical Example #2
In a full wave bridge rectifier circuit, each diode have forward resistance of 2Ω and an infinite reverse resistance. The alternating supply voltage is 230 V RMS and resistive load is 50Ω. Calculate
- (a) Average load current
- (b) Rectifier Efficiency
Solution
The RMS value of supply voltage
$$\mathrm{V_{rms}=230 V}$$
The maximum value of supply voltage
$$\mathrm{V_{m}=230×√2=325.22 V}$$
Maximum value of load current
$$\mathrm{I_{m}=\frac{V}{2R_{d}+R_{L}}=\frac{325.22}{(4+50)}=6.02 A}$$
(a) Average load current
$$\mathrm{I_{avg}=\frac{2l_{m}}{\pi}=\frac{2×6.02}{\pi}=3.83 A}$$
(b) RMS value of load current
$$\mathrm{I_{rms}=\frac{l_{m}}{\sqrt{2}}=\frac{6.02}{\sqrt{2}}=4.26 A}$$
Rectifier efficiency,
$$ \mathrm{\eta=\frac{p_{dc}}{p_{ac}}=\frac{I_{avg^2×{R}𝐿}}{(I_{rms})^2×(2R_{d}+R_{L})}=\frac{3.83^2×50}{4.26^2×54}×100=74.84\%}$$
24K+ Views
