Half Wave Rectifier

Half Wave Rectifier is a diode circuit which is used to transform Alternating Voltage (AC Supply) to Direct Voltage (DC Supply). A single diode is used in the HWR circuit for the transformation of AC to DC.

Half Wave Rectifier circuit allows the one – half cycle of the AC Supply waveform to pass and blocks the other half cycle.

Half Wave Rectifier Circuit Diagram

The circuit of HWR consists of following three main components −

• A Diode

• A Transformer

• A Load (may be a Resistance)

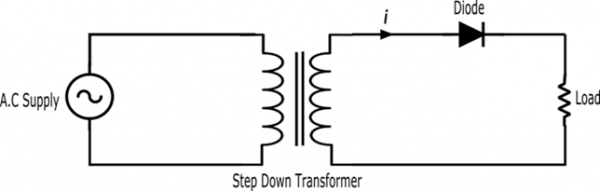
Working of HWR Circuit

Positive Half Cycle

The AC high voltage is applied to the primary of step down transformer and the obtained secondary low voltage is applied to the diode, the diode is forward biased during positive half cycle and act as a short circuit.

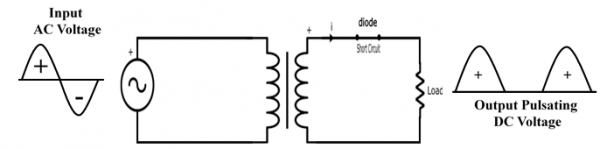
Negative Half Cycle

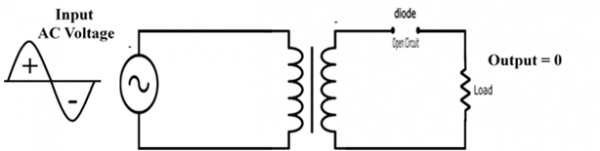
During the negative half cycle, the P – terminal of the diode is connected with the negative supply which reverse biases the diode, the diode behaves like an open circuit and does not produces the output across the load.

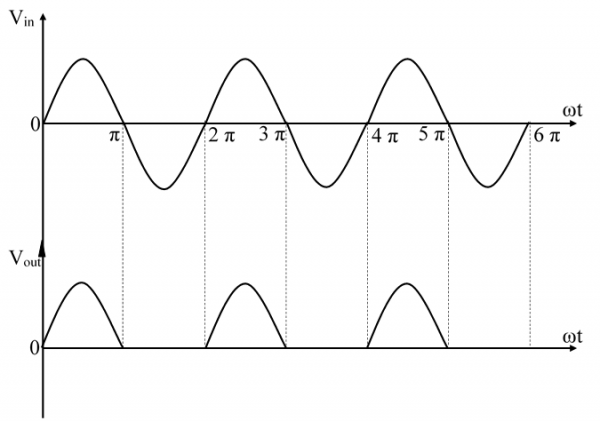
Half Wave Rectifier Waveform

Half Wave Rectifier Formulae

Efficiency of HWR

The efficiency of HWR is defined as the ration output DC power to the input AC power.

$$η=\frac{P_{dc}}{P_{ac}}$$

The maximum efficiency of half wave rectifier is 40.6%.

Peak Inverse Voltage of HWR

The peak inverse voltage of a HWR is the maximum voltage that can a diode withstand without destruction when reverse bias is applied to it.

$\mathrm {PIV} = V_{m}$

RMS Value of Load Current of HWR

$$I_{RMS} = \frac{I_{m}}{2}$$

Average Value of Load Current of HWR

$$I_{avg} = \frac{I_{m}}{π}$$

Form Factor of HWR

$$\mathrm{Form\, Factor}=\frac{\mathrm{RMS\, Value}}{\mathrm{Avg.\,Value}}=\frac{V_{\mathrm{rms}}}{V_{\mathrm{avg}}}$$

For HWR the form factor equals to 1.57

Ripple Factor of HWR

Ripple Factor gives the information about how a HWR can transform input AC voltage to output DC voltage. It is given by

$\mathrm{Ripple\:Factor}=\sqrt{((\mathrm{Form\:Factor})^2 − 1)}$

The ripple factor for half wave rectifier is 1.21.

Application of Half Wave Rectifier

There are some applications of Half Wave Rectifier −

• They are used for rectification
• They are used for demodulation
• They are used for signal peak applications

Disadvantages of Half Wave Rectifier

• The AC supply delivers power only for the half cycle. Therefore, the output is low.
• The pulsating current in the load contains alternating current whose frequency is equal to supply frequency. Therefore, filtering is required to produce steady direct current.

Numerical Example

A diode having internal resistance R_d = 10Ω is used for half wave rectification. If the applied voltage is v = 50 sin⁡(ωt) and load resistance R_L = 10Ω. Find the following −

• I_m, I_dc, I_rms
• AC power input and DC power output
• DC output voltage
• Efficiency of rectification

Solution

Maximum voltage, $V_{m}=50 \, \mathrm{V}$

(a) ${I_{m}=\frac{v_{m}}{R_{d}+R_{L}} = \frac{50}{10+1000}} =0.0495 = 49.5 \thinspace \mathrm {mA}$

${I_{dc}= I_{avg} = \frac{I_{m}}{π}} = \frac{49.5}{π} = 15.76 \thinspace \mathrm {mA}$

${I_{rms} =  \frac{I_{m}}{2}} = \frac{49.5}{2} = 24.75 \thinspace \mathrm {mA}$

(b) $P_{ac}=(I_{\mathrm{rms}})^{2}\: (R_{d}+R_{L})$

$$\Rightarrow P_{ac}=(24.75 \times 10^{-3})^{2} \times  (10 + 1000) = 0.618 \, \mathrm{Watts}$$

     $P_{dc} = (I_{dc})^{2} (R_{L})$

$$\Rightarrow P_{dc} = (15.76 \times 10^{-3})^{2} × (1000) = 0.248 \, \mathrm{Watts}$$

(c) DC output voltage 

$$ = I_{dc} \times R_{L}$$

$$ = (15.76 \times 10^{-3}) \times 1000 = 15.76 \, \mathrm{V}$$

(d) $\mathrm{Efficiency}(\eta)= \frac{P_{dc}}{P_{ac}} = \frac{0.248}{0.618} \times 100 = 40.12%$