Article Categories
- All Categories
-
 Data Structure
Data Structure
-
 Networking
Networking
-
 RDBMS
RDBMS
-
 Operating System
Operating System
-
 Java
Java
-
 MS Excel
MS Excel
-
 iOS
iOS
-
 HTML
HTML
-
 CSS
CSS
-
 Android
Android
-
 Python
Python
-
 C Programming
C Programming
-
 C++
C++
-
 C#
C#
-
 MongoDB
MongoDB
-
 MySQL
MySQL
-
 Javascript
Javascript
-
 PHP
PHP
Fixed Point and Floating Point Number Representations
Digital Computers use Binary number system to represent all types of information inside the computers. Alphanumeric characters are represented using binary bits (i.e., 0 and 1). Digital representations are easier to design, storage is easy, accuracy and precision are greater.
There are various types of number representation techniques for digital number representation, for example: Binary number system, octal number system, decimal number system, and hexadecimal number system etc. But Binary number system is most relevant and popular for representing numbers in digital computer system.
Storing Real Number
These are structures as following below −
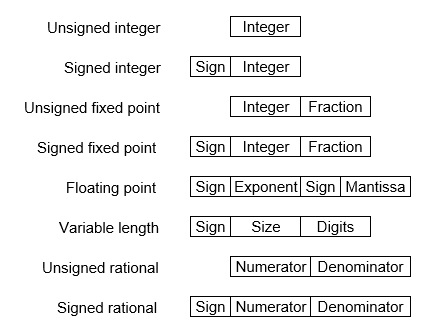
There are two major approaches to store real numbers (i.e., numbers with fractional component) in modern computing. These are (i) Fixed Point Notation and (ii) Floating Point Notation. In fixed point notation, there are a fixed number of digits after the decimal point, whereas floating point number allows for a varying number of digits after the decimal point.
Fixed-Point Representation −
This representation has fixed number of bits for integer part and for fractional part. For example, if given fixed-point representation is IIII.FFFF, then you can store minimum value is 0000.0001 and maximum value is 9999.9999. There are three parts of a fixed-point number representation: the sign field, integer field, and fractional field.
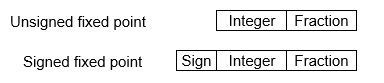
We can represent these numbers using:
- Signed representation: range from -(2(k-1)-1) to (2(k-1)-1), for k bits.
- 1’s complement representation: range from -(2(k-1)-1) to (2(k-1)-1), for k bits.
- 2’s complementation representation: range from -(2(k-1)) to (2(k-1)-1), for k bits.
2’s complementation representation is preferred in computer system because of unambiguous property and easier for arithmetic operations.
Example −Assume number is using 32-bit format which reserve 1 bit for the sign, 15 bits for the integer part and 16 bits for the fractional part.
Then, -43.625 is represented as following:

Where, 0 is used to represent + and 1 is used to represent. 000000000101011 is 15 bit binary value for decimal 43 and 1010000000000000 is 16 bit binary value for fractional 0.625.
The advantage of using a fixed-point representation is performance and disadvantage is relatively limited range of values that they can represent. So, it is usually inadequate for numerical analysis as it does not allow enough numbers and accuracy. A number whose representation exceeds 32 bits would have to be stored inexactly.

These are above smallest positive number and largest positive number which can be store in 32-bit representation as given above format. Therefore, the smallest positive number is 2-16 ≈ 0.000015 approximate and the largest positive number is (215-1)+(1-2-16)=215(1-2-16) =32768, and gap between these numbers is 2-16.
We can move the radix point either left or right with the help of only integer field is 1.
Floating-Point Representation −
This representation does not reserve a specific number of bits for the integer part or the fractional part. Instead it reserves a certain number of bits for the number (called the mantissa or significand) and a certain number of bits to say where within that number the decimal place sits (called the exponent).
The floating number representation of a number has two part: the first part represents a signed fixed point number called mantissa. The second part of designates the position of the decimal (or binary) point and is called the exponent. The fixed point mantissa may be fraction or an integer. Floating -point is always interpreted to represent a number in the following form: Mxre.
Only the mantissa m and the exponent e are physically represented in the register (including their sign). A floating-point binary number is represented in a similar manner except that is uses base 2 for the exponent. A floating-point number is said to be normalized if the most significant digit of the mantissa is 1.
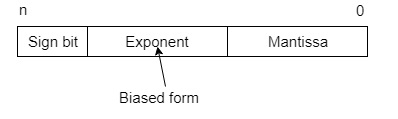
So, actual number is (-1)s(1+m)x2(e-Bias), where s is the sign bit, m is the mantissa, e is the exponent value, and Bias is the bias number.
Note that signed integers and exponent are represented by either sign representation, or one’s complement representation, or two’s complement representation.
The floating point representation is more flexible. Any non-zero number can be represented in the normalized form of ±(1.b1b2b3 ...)2x2n This is normalized form of a number x.
Example −Suppose number is using 32-bit format: the 1 bit sign bit, 8 bits for signed exponent, and 23 bits for the fractional part. The leading bit 1 is not stored (as it is always 1 for a normalized number) and is referred to as a “hidden bit”.
Then −53.5 is normalized as -53.5=(-110101.1)2=(-1.101011)x25 , which is represented as following below,

Where 00000101 is the 8-bit binary value of exponent value +5.
Note that 8-bit exponent ?eld is used to store integer exponents -126 ≤ n ≤ 127.
The smallest normalized positive number that ?ts into 32 bits is (1.00000000000000000000000)2x2-126=2-126≈1.18x10-38 , and largest normalized positive number that ?ts into 32 bits is (1.11111111111111111111111)2x2127=(224-1)x2104 ≈ 3.40x1038 . These numbers are represented as following below,

The precision of a ?oating-point format is the number of positions reserved for binary digits plus one (for the hidden bit). In the examples considered here the precision is 23+1=24.
The gap between 1 and the next normalized ?oating-point number is known as machine epsilon. the gap is (1+2-23)-1=2-23for above example, but this is same as the smallest positive ?oating-point number because of non-uniform spacing unlike in the ?xed-point scenario.
Note that non-terminating binary numbers can be represented in floating point representation, e.g., 1/3 = (0.010101 ...)2 cannot be a ?oating-point number as its binary representation is non-terminating.
IEEE Floating point Number Representation −
IEEE (Institute of Electrical and Electronics Engineers) has standardized Floating-Point Representation as following diagram.
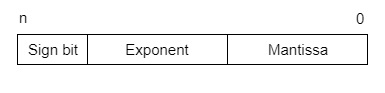
So, actual number is (-1)s(1+m)x2(e-Bias), where s is the sign bit, m is the mantissa, e is the exponent value, and Bias is the bias number. The sign bit is 0 for positive number and 1 for negative number. Exponents are represented by or two’s complement representation.
According to IEEE 754 standard, the floating-point number is represented in following ways:
- Half Precision (16 bit): 1 sign bit, 5 bit exponent, and 10 bit mantissa
- Single Precision (32 bit): 1 sign bit, 8 bit exponent, and 23 bit mantissa
- Double Precision (64 bit): 1 sign bit, 11 bit exponent, and 52 bit mantissa
- Quadruple Precision (128 bit): 1 sign bit, 15 bit exponent, and 112 bit mantissa
Special Value Representation −
There are some special values depended upon different values of the exponent and mantissa in the IEEE 754 standard.
- All the exponent bits 0 with all mantissa bits 0 represents 0. If sign bit is 0, then +0, else -0.
- All the exponent bits 1 with all mantissa bits 0 represents infinity. If sign bit is 0, then +∞, else -∞.
- All the exponent bits 0 and mantissa bits non-zero represents denormalized number.
- All the exponent bits 1 and mantissa bits non-zero represents error.


