Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Explain the operation of DFA with block diagram in TOC
The finite automata (FA) is represented as follows in the theory of computation (TOC) −
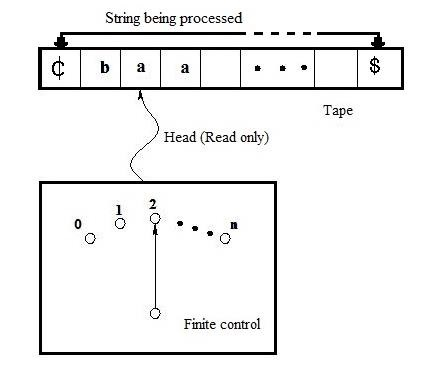
Components of FA
The different components of finite automata are as follows −
Input tape
The input tape has a left end and extends to the right end.
It is divided into blocks and each block containing a single symbol from the input alphabet Σ.
The end block of the tape contains the end markers ₵ at the left end and the end marker $ at the right end.
The absence of end markers indicates that the tape is of infinite length.
The left-to-right sequence of symbols between the two end markers in the input string to be processed.
Read only Head
The tape has a read only head which examines one block at a time and can move one block either to the left or to the right side.
At the beginning of the operation the head is always at the leftmost block of the input tape.
Then the machine restricts the moment of the read only head from left to right direction only and one block every time when it reads symbols.
Finite control
There is a finite control that determines the state of the automaton and also controls the movement of the head.
The input of finite control is usually the symbol under the read head (assumed a) and the present state of the machine (assumed q) to give the following outputs;
A motion of read head along the tape to the next block.
The next state of the finite state machine given by δ(q, a).
Operation of finite automata
A finite automaton or a deterministic at initial time, it is assumed to be that the machine in the initial state q0, with its input mechanism on the leftmost symbol of the input string in input tape.
During every move of the automaton, the input mechanism moves one position to the right, so each move consumes one input symbol.
When the string is reached end, the string is accepted, if the automaton is in one of its final states. Otherwise, it is rejected.
The input mechanism can move only from left to right and reads exactly one symbol on each step.
The transitions from one internal state to another are governed by the transition function δ.
For example, If δ(q0, a) = q1,
Then, if the finite automaton is in state q0 and the current input symbol is a, then the machine will go into the next state q1.
Once it gets to state q1, and then no matter what symbol is read, this machine never leaves state q1 until another input symbol is scanned or accepted.
Example
Check whether string s = {01} is accepted by the machine or not if machine M is defined as
M = ({q0, q1, q2}, {0, 1}, δ, q0{q1}), where δ is given as;
δ (q0, 0) = q0,
δ (q0, 1) = q1,
δ (q1, 0) = q0,
δ (q1, 1) = q2,
δ (q2, 0) = q2,
δ (q2, 0) = q1.
This machine M accepts the string 01. Let’s start from the state q0, the symbol 0 is scanned form the input tape first.
Looking at the edges of the graph, it is clear that the automaton remains in state q0. Next, the read-only head is upgraded by 1 and it reads 1 and the automaton goes into state q1.
We are now at the end of the string and, at the same time, in a final state q1.
1K+ Views
