Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Explain the concept of state elimination method in TOC
There are two methods for converting a Deterministic Finite Automata (DFA) to Regular expression (RE). These methods are as follows −
- Arden's Theorem Method.
- State Elimination Method.
Now, let us learn about the state elimination method used in TOC.
State Elimination Method
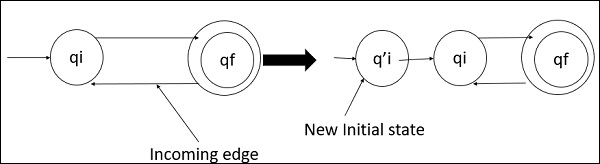
Step 1
- Initial state of DFA does not have any incoming edge.
- If there exists any incoming edge to the initial state, then we need to create a new initial state which has no incoming edge to it.
An example about the relation between incoming edge and initial state is given below−
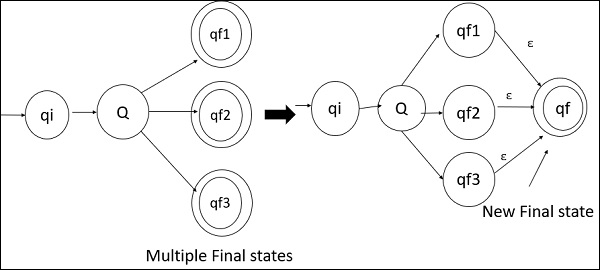
Step 2
- There must be only one final state in DFA.
- If there exist multiple final states in DFA, then we need to convert all final states into non-final states and create a new single final state.
An example of multiple final states and final states is as follows−
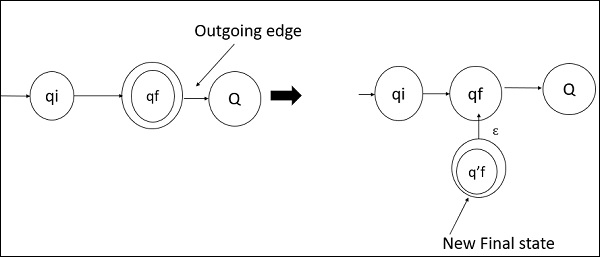
Step 3
- The final state of DFA does not have any outgoing edge
- If there exists any outgoing edge from the final state, then we need to create a new final state which has no outgoing edge from it.
An example of outgoing edge and a new final state is given below −
Step 4
- Eliminate all intermediate states one after the another. These states can be eliminated in any order.
- Finally, only an initial state which is going to the final state will be there
- The cost of this transition is the required Regular Expression.
Updated on: 11-Jun-2021
2K+ Views
Advertisements