Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Diagonal Matrices
Introduction
A diagonal matrix is a matrix in which the entries outside the main diagonal are all zero. Matrices are used in practical life events like military parades, school parades, and planting. The concept of matrix and determinant is recorded as having appeared in the fourth century B.C, although its use is thought to have begun only in the second century BC. Then, towards the end of the seventeenth century, the concept of matrix and determinants came back into use. Mathematical models of everyday world problems are formed as sets of linear equations. Matrices are essential and inevitable to solve these. Mathematicians such as Gauss, Jordan and Hamilton developed matrix theories for studying solutions to sets of linear equations.
Matrices
A Matrix is a rectangular representation of elements in columns and rows closed in parentheses [ ].
Generally, the elements of a Matrix may be real, complex, univariate functions, (i.e. polynomial functions, trigonometric functions and combinations thereof) and multivariate functions.
A matrix π΄ with π πππ€π and π ππππ’πππ can be written as
$$\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n},\:1\leq\:i\:\leq\:m\:,\:1\leq\:j\leq\:n,\:\:that\:is}$$
$$\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$$
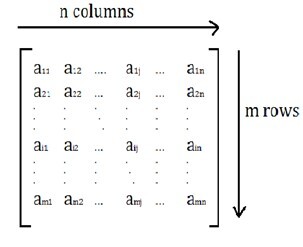
The Order or dimension of the matrix is defined as $\mathrm{m\times\:n}$. That is, π πππ π are the rows and columns present in the matrix.
A Row is defined as a horizontal element in a matrix. A column is defined as a perpendicular element in a matrix.
Types of Matrices
Row and Column matrix
$\mathrm{A\:=\:\begin{bmatrix} A\end{bmatrix}_{1\times\:4}\:=\:\begin{bmatrix} 1 & 0 & 1.1 & \sqrt{2}\\ \end{bmatrix}}$ is a row matrix with order 1 Γ 4. Because the total number of rows in this matrix is one.
If $\mathrm{A\:=\:\begin{bmatrix} A\end{bmatrix}_{1\times\:4}\:=\:\begin{bmatrix} x \\ x\:+\:z \\ 3x \\ 4 \end{bmatrix}}$ it is called a column matrix. Because the total number of columns in this matrix is one
Zero and non-zero Matrix
A matrix $\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$ is called a zero matrix if πππ = 0 for all values $\mathrm{1\leq\:i\leq\:m}$ and $\mathrm{1\leq\:j\leq\:n}$. This will be known as O.
If one element in matrix A is non-zero, then the matrix is known as a non-zero matrix.
Square Matrix
A matrix with a same number of rows and columns, it is called a square matrix. That is, the order of a square matrix is n when a square matrix of $\mathrm{n\times\:n}$ order. For example
$$\mathrm{A\:=\:\begin{bmatrix} a & b & c \\ d & c & f\\ g & h & i \end{bmatrix}}$$
Triangular Matrices
Upper triangular matrix β A matrix with the elements zero below the primary diagonal in a square matrix.
Therefore In a square matrix $\mathrm{B\:=\:\begin{bmatrix} b_{ij}\end{bmatrix}_{m\times\:n},\:if\:b_{ij}\:=\:0,\:j\:<i.}$ Then the matrix is called an upper triangular matrix
$$\mathrm{B\:=\:\begin{bmatrix} 1 & 5 & 7 \\ 0 & 1 & 8\\ 0 & 0 & 2 \end{bmatrix}}$$
Lower triangular matrix β A matrix with the elements zero above the primary diagonal in a square matrix.
Therefore In a square matrix $\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n},\:if\:a_{ij}\:=\:0,\:i\:<i.}$
$$\mathrm{B\:=\:\begin{bmatrix} 2 & 0 & 0 \\ 7 & 6 & 0\\ 3 & 3 & 9 \end{bmatrix}}$$
Diagonal Matrices
The elements $\mathrm{a_{11}\:,\:a_{22}\:,\:a_{33}\:.............,a_{nn}}$ of a square matrix $\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$ of πππππ π are called primary or main diagonal elements
A matrix with elements zero other than the main diagonal elements is called a diagonal matrix.
π΄ π ππ’πππ πππ‘πππ₯ $\mathrm{B\:=\:\begin{bmatrix} b_{ij}\end{bmatrix}_{m\times\:n}\:for\:all\:b_{ij\:=\:0\:,\:i\neq\:j}}$ is called a diagonal matrix. Therefore, in a diagonal matrix, every element are zero other than the main diagonal elements
Types of Diagonal Matrix
Scalar Matrix
It is defined as every primary diagonal element in a diagonal matrix are the same
πΌπ π π ππ’πππ πππ‘πππ₯ $\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$,πΌπ $\mathrm{a_{ij}\:=\:c;i\:=\:j}$ and $\mathrm{a_{ij}\:=\:0;\:i\neq\:j}$ then A is a scalar Matrix. Here c is the standard number.
$$\mathrm{A\:=\:\begin{bmatrix} 2 & 0 & 0 \\ 0 & 2 & 0\\ 0 & 0 & 2 \end{bmatrix}}$$
Identity Matrix
Identity matrix - If every element of a diagonal matrix is zero other than primary diagonal elements are 1.
In a square matrix $\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$, If $\mathrm{a_{ij}\:=\:1;i\:=\:j}$ πππ $\mathrm{a_{ij}\:=\:0;i\:\neq\:j}$ then matrix A is the identity matrix.
$$\mathrm{I\:=\:\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}}$$
Properties of Diagonal Matrices
Adding and multiplying diagonal matrices is very simple. If the primary diagonal elements of a diagonal matrix (starting from the top-left corner) are π1, . . . . . . , ππ, then the matrix operations can be performed by writing the matrix as ππππ (π1, . . . . . . , ππ). The addition and multiplication of two diagonal matrices is
$$\mathrm{A\:=\:\begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix}\:\:\:B\:=\:\begin{bmatrix} c & 0 \\ 0 & d \end{bmatrix}}$$
$$\mathrm{A\:+\:B\:=\begin{bmatrix} a\:+\:c & 0 \\ 0 & b\:+\:d \end{bmatrix}}$$
$$\mathrm{AB\:=\:\begin{bmatrix} ac & 0 \\ 0 & bd \end{bmatrix}}$$
A transpose of a diagonal matrix is applicable when every primary diagonal elements are non-zero.
Applications of Diagonal matrix
Diagonal matrices are widely used in linear algebra
The Linear map is represented by the diagonal matrices. It is desirable to represent the linear map
According to the spectral theorem, a diagonal matrix is similar to a normal matrix.
Solved Examples
1)Find the value of the matrix X?
$$\mathrm{AX\:=\:B}$$
$$\mathrm{A\:=\:\begin{bmatrix} 7 & 0 & 0 \\ 0 & 12 & 0\\ 0 & 0 & 8 \end{bmatrix}\:\:X\:=\begin{bmatrix} x \\ y \\ z \end{bmatrix}\:\:B\:=\begin{bmatrix} 28 \\ 12 \\ 16 \end{bmatrix}}$$
Ans
$$\mathrm{\begin{bmatrix} 7 & 0 & 0 \\ 0 & 12 & 0\\ 0 & 0 & 8 \end{bmatrix}\:\:\begin{bmatrix} x \\ y \\ z \end{bmatrix}\:\:=\:\begin{bmatrix} 28 \\ 12 \\ 16 \end{bmatrix}}$$
$$\mathrm{AX\:=\:\begin{bmatrix} 7x\:+\:0\:+\:0 \\ 0\:+\:12y\:+\:0 \\ 0\:+\:0\:+\:8z \end{bmatrix}}$$
$$\mathrm{AX\:=\begin{bmatrix} 7x \\ 12y \\ 8z \end{bmatrix}}$$
$\mathrm{AX\:=\:B}$, therefore
$$\mathrm{7x\:=\:28}$$
$$\mathrm{12y\:=\:12}$$
$$\mathrm{8z\:=\:16}$$
$$\mathrm{x\:=\:4\:,\:y\:=\:1\:,\:z\:=\:2}$$
$$\mathrm{X\:=\begin{bmatrix} 4 \\ 1 \\ 2 \end{bmatrix}}$$
2)Prove that a matrix A multiplied by an identity matrix will result in the same matrix?
$\mathrm{A\:=\begin{bmatrix} 12 & 8 & 7 \\ 6 & 11 & 3\\ -3 & -1 & 8 \end{bmatrix}}$
Ans
$$\mathrm{A\:=\begin{bmatrix} 12 & 8 & 7 \\ 6 & 11 & 3\\ -3 & -1 & 8 \end{bmatrix}\:\:I\:=\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}}$$
$$\mathrm{AI\:=\:\begin{bmatrix} 12 & 8 & 7 \\ 6 & 11 & 3\\ -3 & -1 & 8 \end{bmatrix}\:\begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1 \end{bmatrix}}$$
$$\mathrm{AI\:=\:\begin{bmatrix} 12 & 8 & 7 \\ 6 & 11 & 3\\ -3 & -1 & 8 \end{bmatrix}}$$
Therefore any matrix multiplied by the identity matrix will result in the same matrix.
Conclusion
Matrices are used in practical life events like military parades, school parades and planting. A Matrix is a rectangular representation of elements in columns and rows closed in parentheses. If one element in matrix A is non-zero, then the matrix is known as a non-zero matrix. Adding and multiplying diagonal matrices is very simple. A matrix with elements zero other than the main diagonal elements is called a diagonal matrix. A transpose of a diagonal matrix is applicable when every primary diagonal elements are non-zero. Diagonal matrices are widely used in linear algebra. The Linear map is represented by the diagonal matrices. It is desirable to represent the linear map. According to the spectral theorem, a diagonal matrix is similar to a normal matrix.
FAQs
1. What is a normal matrix?
A matrix is called a normal matrix if the conjugate transpose matrix and multiplication of a square matrix is commutative.
A square matrix with a real number of elements has the same as the conjugate transpose matrix and its square matrix because the real number of each element is the same element. So all square matrices with real elements are normal.
2. Define conjugate transpose matrix?
The conjugate transpose of a matrix of complex elements is obtained by first transposing the matrix and then replacing each element of the transpose matrix with its complex conjugate.
3. What is the rank of a matrix?
The submatrix and minors of a matrix are necessary to define the rank of a matrix.
The rank of matrix π΅ is the highest order of its non-zero minor determinants.
πβπ ππππ ππ πππ‘πππ₯ π΅ ππ πππππ‘ππ ππ β΄(π΅). The rank of a zero matrix is zero. If there is at least one non-zero element in a matrix then $\mathrm{p(B)\:\geq\:1}$.
4. What are the applications of Matrix?
Matrices are used to represent the values of sets of linear equations.
Matrix codes and their functions are used to produce computer electronic spreadsheets in various fields such as business-related budgeting, pricing of sales plans, and analyzing the results of an experiment in science.
5. Explain transpose of a matrix
The matrix obtained by transposing the columns and rows of matrix π΄ is called the transpose matrix of π΄. It will be marked as π΄π. That is, if $\mathrm{A\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{m\times\:n}}$, then $\mathrm{A^{T}\:=\:\begin{bmatrix} a_{ij}\end{bmatrix}_{n\times\:m}}$.
