Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Sparse Matrices in Data Structure
In this section we will see what is the sparse matrix and how we can represent them in memory. So a matrix will be a sparse matrix if most of the elements of it is 0. Another definition is, a matrix with a maximum of 1/3 non-zero elements (roughly 30% of m x n) is known as sparse matrix.
We use matrices in computers memory to do some operations in an efficient way. But if the matrices are sparse in nature, it may help us to do operations efficiently, but it will take larger space in memory. That spaces have no purpose. So we will follow some other kind of structures to store sparse matrices.
Suppose we have a sparse matrix like below −
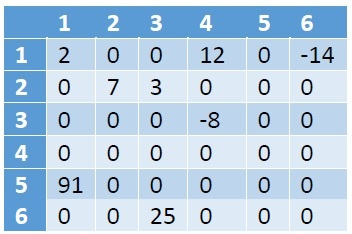
As we can see that there are 8 non-zero elements, and 28 zero-values. This matrix is taking 6*6 = 36 memory spaces. If the size of the matrix is larger, the wastage of space will be increased.
We can store the information about the sparse matrices using table structure. Suppose we will create a table called X like below −
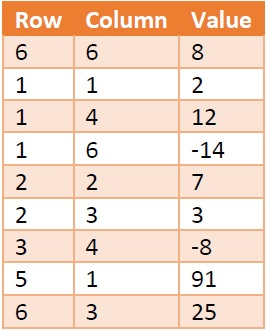
Here the first column is holding the Row number, and second one is holding the column number. The third one is holding the data present at M[row, col]. Each row of this table is called triplets, as there are three parameters. The first triplet is holding the size information of the matrix. Row = 6 and Column = 6 is indicating that the matrix M is 6 x 6 matrix. The value field is denoting the number of non-zero elements present in the array.
This table is also taking 9 * 3 = 36 amount of space, so where is the gain? Well if the matrix size is 8*8 = 64, but only 8 elements are present, then also the table X will take 36 unit of space. We can see that there are fixed 3 columns, the number of rows varies with the number of non-zero elements. So if there are T number of non-zero elements, then the space Complexity will be O(3*T) = O(T). For the matrix it will be O(m x n).
4K+ Views
