Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Depth First Search or DFS for a Graph
The Depth First Search (DFS) is a graph traversal algorithm. In this algorithm one starting vertex is given, and when an adjacent vertex is found, it moves to that adjacent vertex first and try to traverse in the same manner.
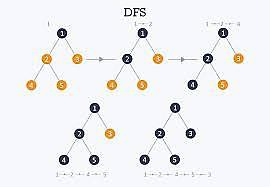
It moves through the whole depth, as much as it can go, after that it backtracks to reach previous vertices to find new path.
To implement DFS in iterative way, we need to use the stack data structure. If we want to do it recursively, external stacks are not needed, it can be done internal stacks for the recursion calls.
Input: The Adjacency matrix of a graph.
A B C D E F A 0 1 1 1 0 0 B 1 0 0 1 1 0 C 1 0 0 1 0 1 D 1 1 1 0 1 1 E 0 1 0 1 0 1 F 0 0 1 1 1 0
Output: DFS Traversal: C F E B D A
Algorithm
dfs(vertices, start)
Input − The list of all vertices, and the start node.
Output − Traverse all nodes in the graph.
Begin initially make the state to unvisited for all nodes push start into the stack while stack is not empty, do pop element from stack and set to u display the node u if u is not visited, then mark u as visited for all nodes i connected to u, do if ith vertex is unvisited, then push ith vertex into the stack mark ith vertex as visited done done End
Example
#include<iostream>
#include<stack>
using namespace std;
#define NODE 6
typedef struct node{
int val;
int state; //status
}node;
int graph[NODE][NODE] = {
{0, 1, 1, 1, 0, 0},
{1, 0, 0, 1, 1, 0},
{1, 0, 0, 1, 0, 1},
{1, 1, 1, 0, 1, 1},
{0, 1, 0, 1, 0, 1},
{0, 0, 1, 1, 1, 0}
};
void dfs(node *vertex, node start){
node u;
stack<node> myStack;
for(int i = 0; i<NODE; i++){
vertex[i].state = 0;//not visited
}
myStack.push(start);
while(!myStack.empty()){
//pop and print node
u = myStack.top();
myStack.pop();
cout << char(u.val+'A') << " ";
if(u.state != 1){
//update vertex status to visited
u.state = 1;
vertex[u.val].state = 1;
for(int i = 0; i<NODE; i++){
if(graph[i][u.val]){
if(vertex[i].state == 0){
myStack.push(vertex[i]);
vertex[i].state = 1;
}
}
}
}
}
}
int main(){
node vertices[NODE];
node start;
char s;
for(int i = 0; i<NODE; i++){
vertices[i].val = i;
}
s = 'C';//starting vertex C
start.val = s-'A';
cout << "DFS Traversal: ";
dfs(vertices, start);
cout << endl;
}Output
DFS Traversal: C F E B D A
Updated on: 05-Aug-2019
830 Views
Advertisements