Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Breadth First Search or BFS for a Graph
The Breadth First Search (BFS) traversal is an algorithm, which is used to visit all of the nodes of a given graph. In this traversal algorithm one node is selected and then all of the adjacent nodes are visited one by one. After completing all of the adjacent vertices, it moves further to check another vertices and checks its adjacent vertices again.
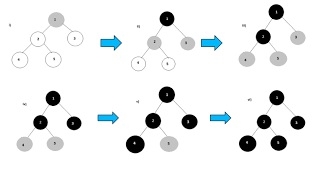
To implement this algorithm, we need to use the Queue data structure. All the adjacent vertices are added into the queue, when all adjacent vertices are completed, one item is removed from the queue and start traversing through that vertex again.
In Graph sometimes, we may get some cycles, so we will use an array to mark when a node is visited already or not.
Input - The Adjacency matrix of the graph.
A B C D E F A 0 1 1 1 0 0 B 1 0 0 1 1 0 C 1 0 0 1 0 1 D 1 1 1 0 1 1 E 0 1 0 1 0 1 F 0 0 1 1 1 0
Output - BFS Traversal: B A D E C F
Algorithm
bfs(vertices, start)
Input − The list of vertices, and the start vertex.
Output − Traverse all of the nodes, if the graph is connected.
Begin define an empty queue que at first mark all nodes status as unvisited add the start vertex into the que while que is not empty, do delete item from que and set to u display the vertex u for all vertices 1 adjacent with u, do if vertices[i] is unvisited, then mark vertices[i] as temporarily visited add v into the queue mark done mark u as completely visited done End
Example
#include<iostream>
#include<queue>
#define NODE 6
using namespace std;
typedef struct node{
int val;
int state; //status
}node;
int graph[NODE][NODE] = {
{0, 1, 1, 1, 0, 0},
{1, 0, 0, 1, 1, 0},
{1, 0, 0, 1, 0, 1},
{1, 1, 1, 0, 1, 1},
{0, 1, 0, 1, 0, 1},
{0, 0, 1, 1, 1, 0}
};
void bfs(node *vert, node s){
node u;
int i, j;
queue<node> que;
for(i = 0; i<NODE; i++){
vert[i].state = 0; //not visited
}
vert[s.val].state = 1;//visited
que.push(s); //insert starting node
while(!que.empty()){
u = que.front(); //delete from queue and print
que.pop();
cout << char(u.val+'A') << " ";
for(i = 0; i<NODE; i++){
if(graph[i][u.val]){
//when the node is non-visited
if(vert[i].state == 0){
vert[i].state = 1;
que.push(vert[i]);
}
}
}
u.state = 2;//completed for node u
}
}
int main(){
node vertices[NODE];
node start;
char s;
for(int i = 0; i<NODE; i++){
vertices[i].val = i;
}
s = 'B';//starting vertex B
start.val = s-'A';
cout << "BFS Traversal: ";
bfs(vertices, start);
cout << endl;
}Output
BFS Traversal: B A D E C F
2K+ Views
