Golang program Breadth-First Search graph

Graph is a data structure that consists of edges or we can say nodes and vertices. Vertices are the lines between the nodes. To traverse all these nodes we have different traversal algorithms. In this article, we will discuss, Breadth − first search or we can say BFS. In Breadth − first search, we first start from one node and move to another till the dead end comes.

Example

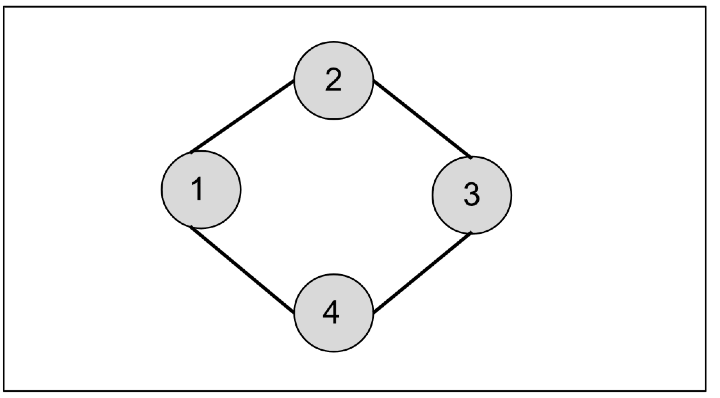
If we start from node 1 then it will first visit node 2 and node 4 first. Then from node 2, we will visit node 3. In this way, the breadth − first search traversal will be 1, 2, 4, and 3.

Algorithm

Step 1:Import the required packages at the top using the import keyword.

Step 2: Then the main function will get run first.

• First, we are declaring and initializing the graph.

• Then we are calling the BFS() function with graph and node as parameters.

Step 3: In the BFS() function below steps will run on each function call.

isvisited := make(map[int]bool)

Create a map that will store the data about whether a node is visited or not.

var bfsQueue Queue

Create a parameter for the queue data structure.

isvisited[node] = true, bfsQueue.Enqueue(node)

Mark the passed node as visited and add the node to the queue.

Run a for loop over all the connected nodes and add to the queue.

Example 1

In this example, we are representing the graph in the form of a matrix and applying a breadth − first search over the matrix. The complexity of this approach will be O(e*e) where e is the number of edges and the space complexity is O(e*e) which is the size of the matrix.

package main

import "fmt"

type Queue struct {
    List []int
}

// function to add element in queue
func (q *Queue) Enqueue(element int) {
    q.List = append(q.List, element)
}

// function to delete element in the queue
func (q *Queue) Dequeue() int {
    if q.isEmpty() {
        fmt.Println("Queue is empty.")
        return 0
    }
    element := q.List[0]
    q.List = q.List[1:]

    return element
}

// function check that queue is empty or not
func (q *Queue) isEmpty() bool {
    return len(q.List) == 0
}

// BFS() is a function with matrix and int value as parameter
func BFS(graph [][]int, node int) {
    // initializing the map that will keep
    // the track is the node is visited or not
    isvisited := make(map[int]bool)

    // creating a Queue variable
    // in which we will add an element at the same level
    // of that node
    var bfsQueue Queue

    // marking current node as visited
    isvisited[node] = true

    // adding a current node in the queue
    bfsQueue.Enqueue(node)

    // running a for loop until the queue becomes empty
    for !bfsQueue.isEmpty() {
        currNode := bfsQueue.List[0]
        fmt.Print(currNode, " ")
        // adding all the connected node in queue if not visted
        for nodes := 0; nodes < len(graph[currNode]); nodes++ {
            if graph[currNode][nodes] == 1 && !isvisited[nodes] {
                bfsQueue.Enqueue(nodes)
                isvisited[nodes] = true
            }
        }
        // removing the current node from queue
        // after visiting
        bfsQueue.Dequeue()
    }
}

func main() {
    // matrix representation of the undirected connected graph
    // where if the value is 1 the node i is connected
    // with node j
    graph := [][]int{{0, 1, 0, 1}, {1, 0, 1, 0}, {0, 1, 0, 1}, {1, 0, 1, 0}}

    fmt.Println("Golang program to do Breath first search of an undirected connected graph represented in the form of a matrix.")

    // calling BFS() function for the breadth-first search
    // traversal of a graph
    BFS(graph, 0)

    fmt.Println()
}

Output

Golang program to do Breath first search of an undirected connected graph represented in the form of a matrix.
0 1 3 2 

Example 2

In this example, we are representing the graph in the form of an adjacency list and applying breadth − first search accordingly. The complexity of this approach will be O(e*v) where e is the number of edges and v is the number of vertices. The space complexity is O(e*v) which is the size of the adjacency list.

package main

import "fmt"

type Queue struct {
    List []int
}

// function to add an element in the queue
func (q *Queue) Enqueue(element int) {
    q.List = append(q.List, element)
}

// function to delete elements in the queue
func (q *Queue) Dequeue() int {
    if q.isEmpty() {
        fmt.Println("Queue is empty.")
        return 0
    }
    element := q.List[0]
    q.List = q.List[1:]

    return element
}

// function checks whether the queue is empty or not
func (q *Queue) isEmpty() bool {
    return len(q.List) == 0
}

// BFS() is a function with matrix and int value as parameter
func BFS(graph [4][]int, node int) {
    //Initializing the map that will keep
    // the track is the node is visited or not
    isvisited := make(map[int]bool)

    // creating a Queue variable
    // in which we will add elements at the same level
    // of that node
    var bfsQueue Queue

    // marking current node as visited
    isvisited[node] = true

    // adding the current node in the queue
    bfsQueue.Enqueue(node)

    // running a for loop until the queue becomes empty
    for !bfsQueue.isEmpty() {
        currNode := bfsQueue.List[0]
        fmt.Print(currNode, " ")
        // adding all the connected nodes in the queue if not visited
        for _, nodes := range graph[currNode] {
            if !isvisited[nodes] {
                bfsQueue.Enqueue(nodes)
                isvisited[nodes] = true
            }
        }
        // removing the current node from queue
        // after visiting
        bfsQueue.Dequeue()
    }
}

func main() {
    //adjacency list representation of the undirected connected graph
    // where if the value is 1 the node i is connected
    // with node j
    var graph [4][]int

    // initializing each list of the array
    graph[0] = []int{1, 3}
    graph[1] = []int{0, 2}
    graph[2] = []int{1, 3}
    graph[3] = []int{0, 2}

    fmt.Println("Golang program to do Breath first search of an undirected connected graph represented in the form of an adjacency list.")

    // calling BFS() function for the breadth-first search
    // traversal of a graph
    BFS(graph, 0)

    fmt.Println()
}

Output

Golang program to do Breath first search of an undirected connected graph represented in the form of an adjacency list.
0 1 3 2 

Conclusion

These are the two different ways of representing graph data structures and running Breadth − first search algorithms. The second method where we are creating an adjacency list is more efficient in terms of time and space both as we are adding those node numbers in the array to which the node is connected. To learn more about Golang you can explore these tutorials.