Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Depth-First Search on a Digraph in Data Structure
The Depth first search for graphs are similar. But for Digraphs or directed graphs, we can find some few types of edges. The DFS algorithm forms a tree called DFS tree. There are four types of edges called −
Tree Edge (T) − Those edges which are present in the DFS tree
Forward Edge (F) − Parallel to a set of tree edges. (From smaller DFS number to larger DFS number, and Larger DFS completion number to Smaller DFS completion number)
Backward Edge (B) − From larger DFS number to Smaller DFS number and Smaller DFS completion number to Larger DFS completion number.
Cross Edge (C) − Larger DFS number to Smaller DFS number, and Larger DFS completion number to Smaller DFS completion number.
Suppose we have a graph like below −
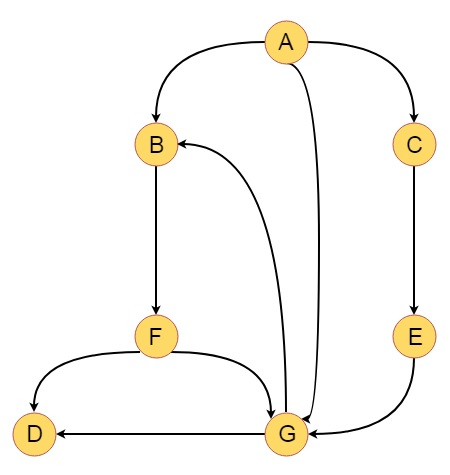
Now we will perform DFS by taking A as initial vertex, and put the DFS number and DFS completion numbers. So the tree will be look like below −
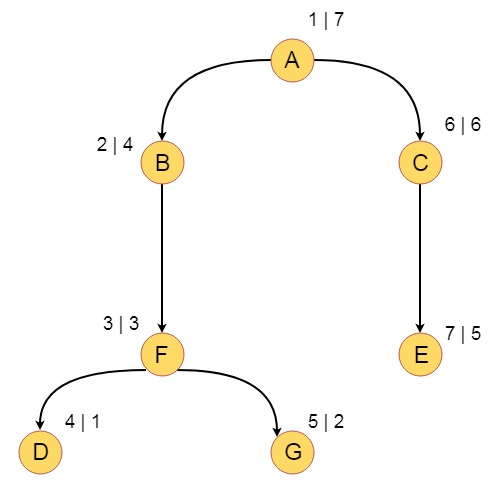
So the DFS traversal is A, B, F, D, G, C, E
The Tree edges are − T = {(A, B), (B, F), (F, D), (F, G), (A, C), (C, E)}
The Forward edges are − F = {(A, G)}
The Backward edges are − B = {(G, B)}
The Cross edges are −C = {(G, D)}
412 Views
