Check if a given graph is Bipartite using DFS in C++ program

Suppose we have a connected graph; we have to check whether the graph is bipartite or not. If the graph coloring is possible applying two colors such that nodes in a set are colored with the same color.

So, if the input is like

then the output will be True

To solve this, we will follow these steps −

Define a function insert_edge(), this will take an edge array adj, u, v,
insert v at the end of adj[u]
insert u at the end of adj[v]
From the main method do the following,
for each u in adj[v],do
- if visited[u] is same as false, then −
  - visited[u] := true
  - color[u] := invert of color[v]
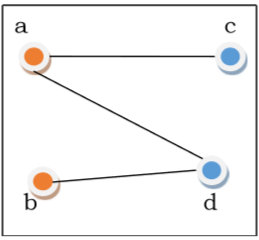
  - if not is_bipartite_graph(adj, u, visited, color), then −
    - return false
- otherwise when color[u] is same as color[v], then −
  - return false
return true

Example (C++)

Let us see the following implementation to get better understanding −

Live Demo

#include <bits/stdc++.h>
using namespace std;
void insert_edge(vector<int> adj[], int u, int v){
   adj[u].push_back(v);
   adj[v].push_back(u);
}
bool is_bipartite_graph(vector<int> adj[], int v, vector<bool>& visited, vector<int>& color){
   for (int u : adj[v]) {
      if (visited[u] == false) {
         visited[u] = true;
         color[u] = !color[v];
         if (!is_bipartite_graph(adj, u, visited, color))
            return false;
      }
      else if (color[u] == color[v])
      return false;
   }
   return true;
}
int main() {
   int N = 6;
   vector<int> adj_list[N + 1];
   vector<bool> visited(N + 1);
   vector<int> color(N + 1);
   insert_edge(adj_list, 1, 2);
   insert_edge(adj_list, 2, 3);
   insert_edge(adj_list, 3, 4);
   insert_edge(adj_list, 4, 5);
   insert_edge(adj_list, 5, 6);
   insert_edge(adj_list, 6, 1);
   visited[1] = true;
   color[1] = 0;
   cout << (is_bipartite_graph(adj_list, 1, visited, color));
}

Input

insert_edge(adj_list, 1, 2);
insert_edge(adj_list, 2, 3);
insert_edge(adj_list, 3, 4);
insert_edge(adj_list, 4, 5);
insert_edge(adj_list, 5, 6);
insert_edge(adj_list, 6, 1);