Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program to Perform Left Rotation on a Binary Search Tree
A Binary Search Tree is a sorted binary tree in which all the nodes have following two properties −
The right sub-tree of a node has all keys greater than to its parent node's key.
The left sub-tree of a node has all keys less than to its parent node's key. Each node should not have more than two children.
Tree rotation is an operation that changes the structure without interfering with the order of the elements on a binary tree. It moves one node up in the tree and one node down. It is used to change the shape of the tree, and to decrease its height by moving smaller subtrees down and larger subtrees up, resulting in improved performance of many tree operations. The direction of a rotation depends on the side which the tree nodes are shifted upon whilst others say that it depends on which child takes the root’s place. This is a C++ program to perform Left Rotation on a Binary Search Tree.
Function Description:
height(avl *) : It calculate the height of the given AVL tree.
difference(avl *): It calculate the difference between height of sub trees of given tree
avl *rr_rotat(avl *): A right-right rotation is a combination of right rotation followed by right rotation.
avl *ll_rotat(avl *): A left-left rotation is a combination of left rotation followed by left rotation.
avl *lr_rotat(avl*): A left-right rotation is a combination of left rotation followed by right rotation.
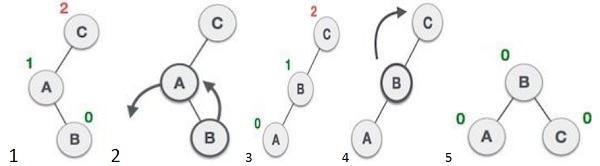
avl *rl_rotat(avl *): It is a combination of right rotation followed by left rotation.
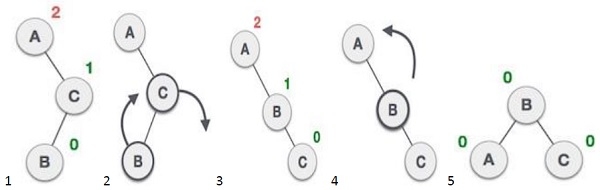
avl * balance(avl *): It perform balance operation to the tree by getting balance factor
avl * insert(avl*, int): It perform insert operation. Insert values in the tree using this function.
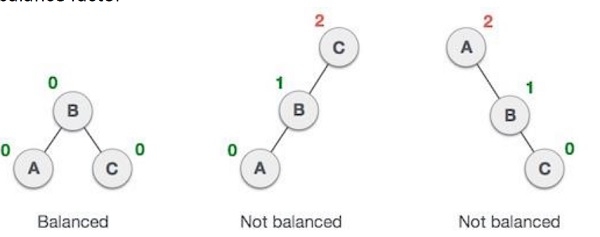
show(avl*, int): It display the values of the tree.
inorder(avl *): Traverses a tree in an in-order manner.
preorder(avl *): Traverses a tree in a pre-order manner.
postorder(avl*): Traverses a tree in a post-order manner.
Example
#include<iostream>
#include<cstdio>
#include<sstream>
#include<algorithm>
#define pow2(n) (1 << (n))
using namespace std;
struct avl {
int d;
struct avl *l;
struct avl *r;
}*r;
class avl_tree {
public:
int height(avl *);
int difference(avl *);
avl *rr_rotat(avl *);
avl *ll_rotat(avl *);
avl *lr_rotat(avl*);
avl *rl_rotat(avl *);
avl * balance(avl *);
avl * insert(avl*, int);
void show(avl*, int);
void inorder(avl *);
void preorder(avl *);
void postorder(avl*);
avl_tree() {
r = NULL;
}
};
int avl_tree::height(avl *t) {
int h = 0;
if (t != NULL) {
int l_height = height(t->l);
int r_height = height(t->r);
int max_height = max(l_height, r_height);
h = max_height + 1;
}
return h;
}
int avl_tree::difference(avl *t) {
int l_height = height(t->l);
int r_height = height(t->r);
int b_factor = l_height - r_height;
return b_factor;
}
avl *avl_tree::rr_rotat(avl *parent) {
avl *t;
t = parent->r;
parent->r = t->l;
t->l = parent;
cout<<"Right-Right Rotation";
return t;
}
avl *avl_tree::ll_rotat(avl *parent) {
avl *t;
t = parent->l;
parent->l = t->r;
t->r = parent;
cout<<"Left-Left Rotation";
return t;
}
avl *avl_tree::lr_rotat(avl *parent) {
avl *t;
t = parent->l;
parent->l = rr_rotat(t);
cout<<"Left-Right Rotation";
return ll_rotat(parent);
}
avl *avl_tree::rl_rotat(avl *parent) {
avl *t;
t= parent->r;
parent->r = ll_rotat(t);
cout<<"Right-Left Rotation";
return rr_rotat(parent);
}
avl *avl_tree::balance(avl *t) {
int bal_factor = difference(t);
if (bal_factor > 1) {
if (difference(t->l) > 0)
t = ll_rotat(t);
else
t = lr_rotat(t);
}
else if (bal_factor < -1) {
if (difference(t->r) > 0)
t= rl_rotat(t);
else
t = rr_rotat(t);
}
return t;
}
avl *avl_tree::insert(avl *r, int v) {
if (r == NULL) {
r= new avl;
r->d = v;
r->l = NULL;
r->r= NULL;
return r;
}
else if (v< r->d) {
r->l= insert(r->l, v);
r = balance(r);
}
else if (v >= r->d) {
r->r= insert(r->r, v);
r = balance(r);
}
return r;
}
void avl_tree::show(avl *p, int l) {
int i;
if (p != NULL) {
show(p->r, l+ 1);
cout<<" ";
if (p == r)
cout << "Root -> ";
for (i = 0; i < l&& p != r; i++)
cout << " ";
cout << p->d;
show(p->l, l + 1);
}
}
void avl_tree::inorder(avl *t) {
if (t == NULL)
return;
inorder(t->l);
cout << t->d << " ";
inorder(t->r);
}
void avl_tree::preorder(avl *t) {
if (t == NULL)
return;
cout << t->d << " ";
preorder(t->l);
preorder(t->r);
}
void avl_tree::postorder(avl *t) {
if (t == NULL)
return;
postorder(t ->l);
postorder(t ->r);
cout << t->d << " ";
}
int main() {
int c, i;
avl_tree avl;
while (1) {
cout << "1.Insert Element into the tree" << endl;
cout << "2.show Balanced AVL Tree" << endl;
cout << "3.InOrder traversal" << endl;
cout << "4.PreOrder traversal" << endl;
cout << "5.PostOrder traversal" << endl;
cout << "6.Exit" << endl;
cout << "Enter your Choice: ";
cin >> c;
switch (c) {
case 1:
cout << "Enter value to be inserted: ";
cin >> i;
r= avl.insert(r, i);
break;
case 2:
if (r == NULL) {
cout << "Tree is Empty" << endl;
continue;
}
cout << "Balanced AVL Tree:" << endl;
avl.show(r, 1);
cout<<endl;
break;
case 3:
cout << "Inorder Traversal:" << endl;
avl.inorder(r);
cout << endl;
break;
case 4:
cout << "Preorder Traversal:" << endl;
avl.preorder(r);
cout << endl;
break;
case 5:
cout << "Postorder Traversal:" << endl;
avl.postorder(r);
cout << endl;
break;
case 6:
exit(1);
break;
default:
cout << "Wrong Choice" << endl;
}
}
return 0;
}Output
1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 13 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 10 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 15 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 5 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 11 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 4 Left-Left Rotation1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 8 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 3 Inorder Traversal: 4 5 8 10 11 13 15 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 4 Preorder Traversal: 10 5 4 8 13 11 15 16 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 5 Postorder Traversal: 4 8 5 11 16 15 13 10 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 14 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 3 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 7 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 9 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 1 Enter value to be inserted: 52 Right-Right 1.Insert Element into the tree 2.show Balanced AVL Tree 3.InOrder traversal 4.PreOrder traversal 5.PostOrder traversal 6.Exit Enter your Choice: 6
2K+ Views
