Clustering in Machine Learning

In machine learning, clustering is a fundamental method that is crucial for extracting knowledge from datasets and spotting hidden patterns. Clustering techniques let us search through massive volumes of data and find significant structures by putting related data points together. This procedure helps with data exploration, segmentation, and comprehension of intricate connections between data pieces. We can extract important insights from unlabeled data by autonomously locating clusters without the requirement for predetermined labels. Customer segmentation, anomaly detection, picture and document organization, and genomics research are just a few of the real−world applications where clustering is crucial. We'll be looking closely at clustering in machine learning in this post.

Understanding clustering

The process of assembling related data points based on their intrinsic traits is known as clustering, and it is a fundamental machine−learning approach. Without the use of labels or categories, clustering aims to uncover underlying patterns, structures, and relationships in datasets. Clustering falls within the category of unsupervised learning, which uses unlabeled data instead of labeled data to achieve its goal of exploration and knowledge discovery.

Data points in the context of clustering refer to specific instances or observations within a dataset. A collection of traits or properties that accurately reflect these data pieces' characteristics serve as their representation. As a key idea in clustering, the similarity between data points indicates how similar or related they are based on their feature values. While taking into account both the size and the direction of variation across attributes, dissimilarity quantifies the degree of variance between data points.

Types of Clustering

K−means Clustering

One of the most well−known and straightforward clustering methods is K−means clustering. The data will be divided into K unique clusters, where K is a predetermined value. The method updates the centroids until convergence is reached before iteratively assigning data points to the closest centroid (representative point). For big datasets, K−means clustering is effective, although it is sensitive to the initial selection of centroids.

Here is the code example:

from sklearn.cluster import KMeans
import matplotlib.pyplot as plt

# Creating a sample dataset for K-means clustering
X = [[1, 2], [1.5, 1.8], [5, 8], [8, 8], [1, 0.6], [9, 11]]

# Applying K-means clustering with K=2
kmeans = KMeans(n_clusters=2)
kmeans.fit(X)

# Visualizing the clustering result
labels = kmeans.labels_
centroids = kmeans.cluster_centers_

for i in range(len(X)):
   plt.scatter(X[i][0], X[i][1], c='blue' if labels[i] == 0 else 'red')

plt.scatter(centroids[:, 0], centroids[:, 1], marker='x', s=150, linewidths=5, c='black')
plt.show()

Output

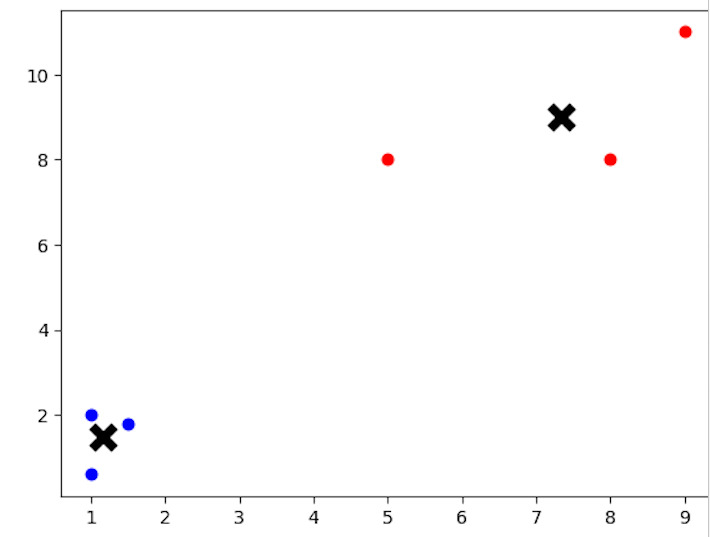
A sample dataset represented by the variable X is subjected to the K-means clustering technique in the code. The clustering is carried out using the KMeans class from the scikit−learn toolkit. 6 data points with 2−dimensional coordinates are present in this example's dataset. We tell the algorithm to look for two clusters in the data by setting n_clusters=2. Following the K−means model's fitting, the code plots the data points and centroids, with each data point colored according to its allocated cluster, to show the clustering outcome.

Hierarchical clustering

By progressively merging or splitting clusters, hierarchical clustering arranges them into a hierarchy. The two main categories under which it can be classified are agglomerative and divisive clustering. Aggregative clustering starts by considering each data point as a separate cluster, and then gradually combines the most similar clusters until only one cluster remains.

On the other hand, starting with the entire dataset as a single cluster and recursively splitting into smaller clusters in divisive clustering leads to the generation of distinct clusters for each data point.

Here is the code example:

from sklearn.cluster import AgglomerativeClustering
import matplotlib.pyplot as plt
import numpy as np

# Creating a sample dataset for hierarchical clustering
np.random.seed(0)
X = np.random.randn(10, 2)

# Applying hierarchical clustering
hierarchical = AgglomerativeClustering(n_clusters=2)
hierarchical.fit(X)

# Visualizing the clustering result
labels = hierarchical.labels_

for i in range(len(X)):
   plt.scatter(X[i, 0], X[i, 1], c='blue' if labels[i] == 0 else 'red')

plt.show()

Output

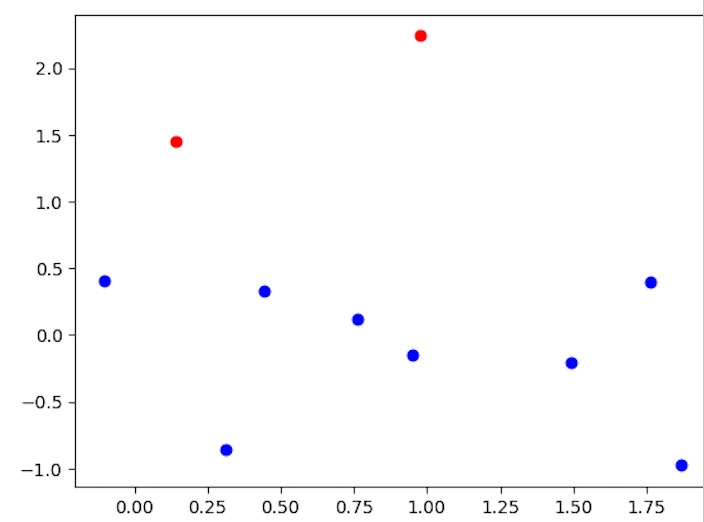
Using the Scikit−Learn AgglomerativeClustering class, the code illustrates hierarchical clustering. It creates a sample dataset, represented by the variable X, with 10 data points and 2-dimensional coordinates. The required number of clusters, n_clusters=2, is applied to the hierarchical clustering method. The code then plots the data points, coloring each one according to its allocated cluster, to see the clustering result.

Density−Based Clustering (DBSCAN)

DBSCAN (Density−Based Spatial Clustering of Applications with Noise), for example, finds clusters based on the density of data points in the feature space. While classifying data points in sparse areas as noise or outliers, it clusters together data points that are reasonably near and dense. When dealing with unevenly formed clusters and variable cluster densities, density−based clustering is quite successful.

Here is the code example:

from sklearn.cluster import DBSCAN
import matplotlib.pyplot as plt
import numpy as np

# Creating a sample dataset for density-based clustering
np.random.seed(0)
X = np.concatenate((np.random.randn(10, 2) + 2, np.random.randn(10, 2) - 2))

# Applying DBSCAN clustering
dbscan = DBSCAN(eps=0.6, min_samples=2)
dbscan.fit(X)

# Visualizing the clustering result
labels = dbscan.labels_

for i in range(len(X)):
   plt.scatter(X[i, 0], X[i, 1], c='blue' if labels[i] == 0 else 'red')

plt.show()

Output

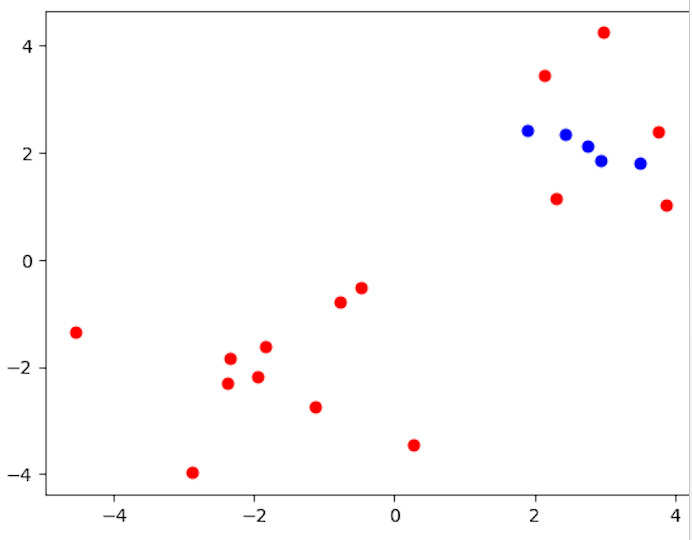
Utilizing the DBSCAN class from scikit−learn, the code illustrates density−based clustering. It generates a sample dataset of 20 2-dimensional data points, which is represented by the variable X. When using the DBSCAN method, the parameters eps=0.6 (the greatest distance between two samples for them to be regarded as belonging to the same neighborhood) and min_samples=2 (the minimal number of samples in a neighbourhood for a point to be regarded as a core point) are used. The code then plots the data points, colouring each one according to the cluster to which it belongs, to see the clustering result.

Conclusion

Clustering is essential for obtaining insightful information from datasets and spotting hidden patterns. Clustering techniques simplify different applications across disciplines and enable data−driven decision−making by automatically grouping related data pieces. We are able to harness the potential of clustering in machine learning, opening up new possibilities for knowledge discovery and creativity, by comprehending the various clustering algorithms, using suitable evaluation metrics, and putting them to use in practical situations.