CDMA - Techniques

Rake Receiver

Due to the reflection on the challenges of a broadband, radio channel can consists of many copies (multipath), signals originally transmitted with different amplitude, phase, and delay. If the signal components arrive over a chip period of each other, a rake receiver may be used to adjust and combine. The Rake receiver uses a principle of diversity through multiple paths. The figure given below shows the Rake receiver scheme.

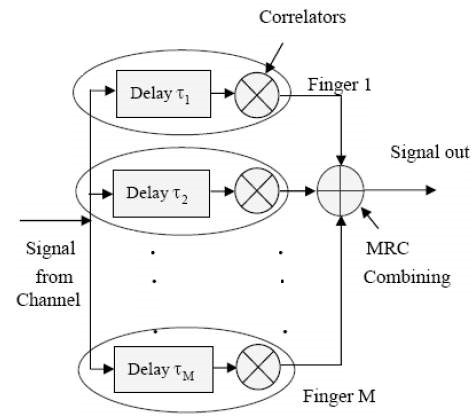
The Rake receiver processes several multipath signals components. The correlator outputs are combined to achieve better reliability and communication performance. Bit decision on the basis of a single correlation can produce a large bit error rate as multipath component processed by the fact that the correlator can be damaged by discoloration. If the output of a correlator is corrupted by fading, the other cannot be, and the corrupt signal can be reduced by the weighting process.

Walsh Code

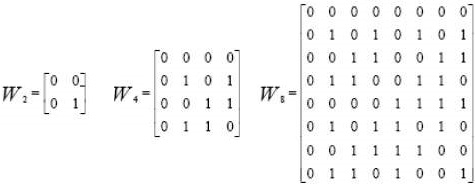
Walsh Codes are most commonly used in the orthogonal codes of CDMA applications. These codes correspond to lines of a special square matrix called the Hadamard matrix. For a set of Walsh codes of length N, it consists of n lines to form a square matrix of n × n Walsh code.

The IS-95 system uses 64 Walsh function matrix 64. The first line of this matrix contains a string of all zeros with each of the following lines containing different combinations of bit 0 and 1. Each line is orthogonal and equal representation for binary bits. When implemented with the CDMA system, each mobile user uses one of the 64 sequences of rows in the matrix as a spreading code. And, it provides zero cross-correlation among all the other users. This matrix is defined recursively as follows −

Where n is a power of 2 and indicates the different dimensions of the matrix W. Further, n represents the logic NOT operation on all bits in this matrix. The three matrices W_2, W_4, and W_8, respectively show the Walsh function for the dimension 2, 4, and 8.

Each line of the 64 Walsh matrix 64 corresponds to a channel number. The channel number 0 is mapped to the first row of the Walsh matrix, which is the code of all zeros. This channel is also known as the pilot channel and is used to form and to estimate the impulse response of a mobile radio channel.

To calculate the cross-correlation between the sequences, we will need to convert the bits into the matrix to form the antithesis of ± 1 values. However, all users on the same CDMA channel can be synchronized with an accuracy of one chip interval using a common long PN sequence. It also functions as a data scrambler.

Walsh Code is a group of spreading codes having good autocorrelation properties and poor cross correlation properties. Walsh codes are the backbone of CDMA systems and are used to develop the individual channels in CDMA.
For IS-95, there are 64 codes available.
- Code `0’ is used as the pilot and code `32’ is used for synchronization.
- Codes 1 through 7 are used for control channels, and the remaining codes are available for traffic channels. Codes 2 to 7 are also available for traffic channels if they are not needed.
For cdma2000, multitude of Walsh codes exist, which vary in length to accommodate the different data rates and Spreading Factors of the different Radio Configurations.
One of the 64 orthogonal bit pattern at a rate of 1.2288 Mcps.
Walsh codes are used to identify the data for each individual transmission. In the forward link, they define forward code channels within a CDMA frequency.
In the reverse link, all 64 codes are used by each reverse channel to carry information.

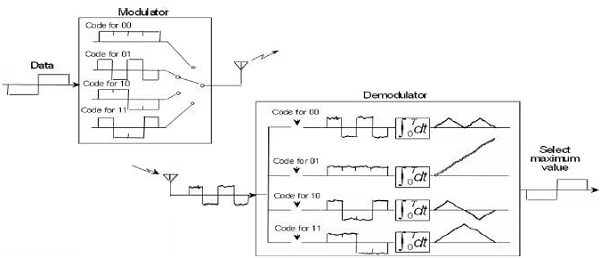
Take a look at the following illustration. It shows how multiplexing is carried out using Walsh Code.