Teach with us

C Program to build DFA accepting the languages ending with “01”

Data Structure AlgorithmsComputer ScienceComputers

Problem

Design deterministic finite automata (DFA) with ∑ = {0, 1} that accepts the languages ending with “01” over the characters {0, 1}.

Solution

The strings that are generated for a given language are as follows −

L={01,001,101,110001,1001,……….}

The minimum length of the string is 2, the number of states that the DFA consists of for the given language is: 2+1 = 3 states.

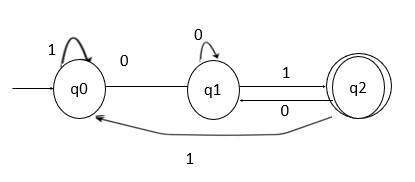
Here,

  • q0 − On input 0 it goes to state q1 and on input 1 it goes to itself.

  • q1 − On input 0 it goes to itself and on input 1 it goes to State q2.

  • q2 − On input 0 it goes to State q1 and on input 1 goes to State q0. State to q2 is the final state.

Example

Following is the C program to construct a DFA with ∑ = {0, 1} that accepts the languages ending with “01” over the characters {0, 1} -

 Live Demo

#include
#define max 100
main() {
   char str[max],f='a';
   int i;
   printf("enter the string to be checked: ");
   scanf("%s",str);
   for(i=0;str[i]!='\0';i++) {
      switch(f) {
         case 'a': if(str[i]=='0') f='b';
            else if(str[i]=='1') f='a';
         break;
         case 'b': if(str[i]=='0') f='b';
            else if(str[i]=='1') f='c';
         break;
         case 'c': if(str[i]=='0') f='b';
            else if(str[i]=='1') f='a';
         break;
      }
   }
   if(f=='c')
      printf("\nString is accepted", f);
   else printf("\nString is not accepted", f);
      return 0;
}

Output

The output is as follows −

Run 1:
enter the string to be checked: 10101001
String is accepted.
Run 2:
enter the string to be checked: 10000010
String is not accepted.
raja
Bhanu Priya
Updated on 15-Jun-2021 12:03:41

Previous Page Print Page Next Page  
Advertisements