Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C program for DFA accepting all strings over w ∈(a,b)* containing “aba” as a substring
Problem
Design a DFA for the language L={w1abaw2 | w1,w2 Є(a,b)*}, which means the DFA accepts all strings which contain “aba” as a substring.
Solution
The strings that are accepted by language L= {aba,aabaa, aabab, babab, ababa, …….}
Step 1 − Transition diagram for minimal string (starting string) −
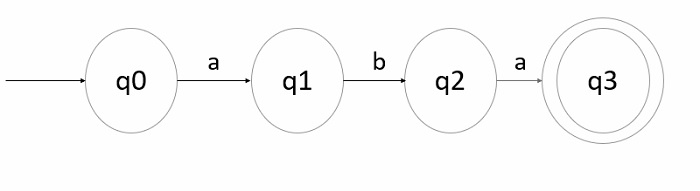
If w1 and w2 are null then the string it generates is “aba” because w1, w2 ε(a,b)*
q0 is the initial state and q3 is the final state.
Step 2 − The final DFA for the given language is as follows −
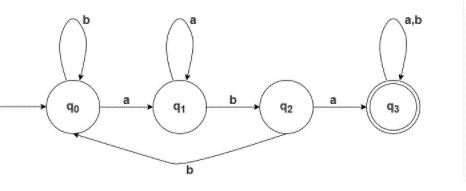
Explanation
qo is the initial state q0 on ‘a’ goes to q1 and on ‘b’ goes to q0, according to DFA each state has to generate a transition on both inputs.
q1 on ‘a’ goes to q1 and on ‘b’ goes to q2, we have to keep in mind according to the given language we need to generate a substring “aba”.
q2 on ‘a’ goes on q3 on ‘b’ goes to q0 state.
q3 which is the final state, on input ‘a’ and ‘b’ goes to q3 only.
Transition Table
Let’s see the transition table as follows −
| Current state | Input a | Input b |
|---|---|---|
| q0 | q1 | q0 |
| q1 | q1 | q2 |
| q2 | q3 | q0 |
| *q3 | q3 | q3 |
Example
Following is the C program for construction of DFA accepting all strings over w ε(a,b)* which contains “aba” as a substring -
#include <stdio.h>
#include <string.h>
void checkDFA(char s[] ) {
// storing initial state
int initialState = 0;
//assign initial state to previous state.
int previousState = initialState;
int finalState;
for(int i = 0; i < strlen(s); i++) {
if((previousState == 0 && s[i] == 'a') || (previousState == 1 && s[i] == 'a')) {
finalState = 1;
}
if((previousState == 0 && s[i] == 'b') || (previousState == 2 && s[i] == 'b')) {
finalState = 0;
}
if(previousState == 1 && s[i] == 'b') {
finalState = 2;
}
if((previousState == 2 && s[i] == 'a') || (previousState == 3)) {
finalState = 3;
}
previousState = finalState;
}
if(finalState == 3) {
printf("given string is Accepted");
}
else
{
printf("given string is Not Accepted");
}
}
int main() {
// Given string
char s[40];
printf("implementation of DFA which having a sub string 'aba':
enter a string:");
scanf("%s",s);
checkDFA(s);
return 0;
}Output
The output is as follows −
Run 1: implementation of DFA which having a sub string 'aba': enter a string:aba given string is Accepted. Run 2: implementation of DFA which having a sub string 'aba': enter a string:abba given string is Not Accepted.
2K+ Views
