
- Basics of Computers – Home
- Basics of Computers – Introduction
- Basics of Computers - Classifications
- Basics of Computers – S/W Concepts
- Basics of Computers – System S/W
- Functions of Operating System
- Types of Operating System
- Basics of Computers – Utility S/W
- Open Source Software
- Basics of Computers – Office Tools
- Domain Specific Tools
- Number System
- Number System Conversion
- Microprocessor Concepts
- Evolution of Microprocessor
- Primary Memory
- Secondary Memory
- Basics of Computers – I/O Ports
Number System Conversion
As you know decimal, binary, octal and hexadecimal number systems are positional value number systems. To convert binary, octal and hexadecimal to decimal number, we just need to add the product of each digit with its positional value. Here we are going to learn other conversion among these number systems.
Decimal to Binary
Decimal numbers can be converted to binary by repeated division of the number by 2 while recording the remainder. Lets take an example to see how this happens.
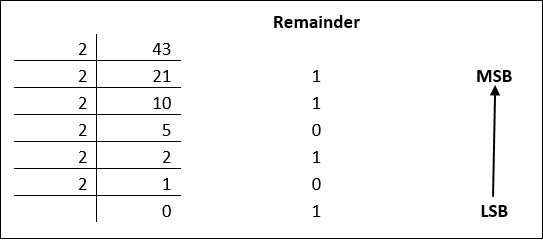
The remainders are to be read from bottom to top to obtain the binary equivalent.
4310 = 1010112
Decimal to Octal
Decimal numbers can be converted to octal by repeated division of the number by 8 while recording the remainder. Lets take an example to see how this happens.

Reading the remainders from bottom to top,
47310 = 7318
Decimal to Hexadecimal
Decimal numbers can be converted to octal by repeated division of the number by 16 while recording the remainder. Lets take an example to see how this happens.

Reading the remainders from bottom to top we get,
42310 = 1A716
Binary to Octal and Vice Versa
To convert a binary number to octal number, these steps are followed −
Starting from the least significant bit, make groups of three bits.
If there are one or two bits less in making the groups, 0s can be added after the most significant bit
Convert each group into its equivalent octal number
Lets take an example to understand this.
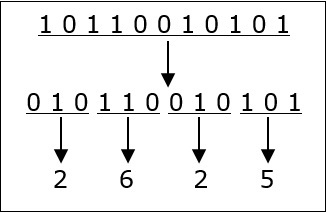
101100101012 = 26258
To convert an octal number to binary, each octal digit is converted to its 3-bit binary equivalent according to this table.
| Octal Digit | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Binary Equivalent | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
546738 = 1011001101110112
Binary to Hexadecimal
To convert a binary number to hexadecimal number, these steps are followed −
Starting from the least significant bit, make groups of four bits.
If there are one or two bits less in making the groups, 0s can be added after the most significant bit.
Convert each group into its equivalent octal number.
Lets take an example to understand this.
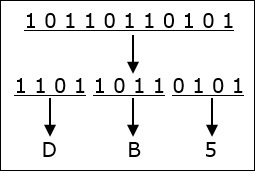
101101101012 = DB516
To convert an octal number to binary, each octal digit is converted to its 3-bit binary equivalent.