Area of circle inscribed within rhombus?

Circle inscribed in a rhombus touches its four side a four ends. The side of rhombus is a tangent to the circle.

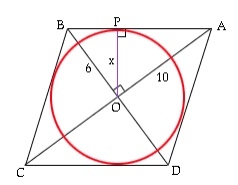
Here, r is the radius that is to be found using a and, the diagonals whose values are given.

Now the area of triangle AOB = ½ * OA * OB = ½ * AB * r (both using formula ½*b*h).

½ *a/2*b/2 = ½ *( √ (a²/4 + b²/4))*r

a*b/8 = √ (a²+ b² )*r /4

r = a*b/ 2√ (a²+ b² )

Area of circle = π*r*r = π*(a²*b²)/4(a²+ b² )

Example

The diagonal of the rhombus 5 & 10.

Area is 15.700000

Example Code

 Live Demo

#include <stdio.h>
int main(void) {
   int a = 5; int b= 10;
   float pie = 3.14;
   float area = (float)((pie*a*a*b*b)/(4*((a*a)+(b*b))));
   printf("The area of circle inscribed in the rhombus of diagonal %d and %d is %f",a,b,area);
   return 0;
}

Output

The area of circle inscribed in the rhombus of diagonal 5 and 10 is 15.700000