Swift Program to Calculate Area of Circle Inscribed in Square

This tutorial will discuss how to write swift program to calculate area of circle inscribed in square.

We have a figure in which a circle is inscribed in a square. Which means the centre of the circle and the square is same and the diameter of the circle is equal to the length of the side of the square. If we have at least one measurement of square or the circle, then we can easily calculate the area and perimeter of the square, or area and circumference and area of the circle.

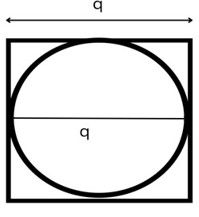
Here we find the area of the circle inscribe in the square using the following formula −

(丌/4)*q*q

Here, q is the radius of the circle and side of the square.

Derivation of the above Formula:

Suppose q is the side of the square

Area of the circle is 丌r2.

As we known that the side and the diameter of the circle is equal. So, the radius is −

r = q/2

Hence the area of the circle inscribed in square is −

A = 丌(q/2)2 = (丌/4)q2

Below is a demonstration of the same −

Input

Suppose our given input is −

side = 15

Output

The desired output would be −

Area of the circle inscribed in square = 176.71458676442586

Algorithm

Following is the algorithm −

Step 1 - Create a function with return value.

Step 2 - Find the area of the circle inscribe in square using the following formula:

return (Double.pi/4) * q * q

Step 3 - Calling the function and pass the side in the circle as a parameter.

Step 4 - Print the output.

Example

The following program shows how to calculate the area of circle inscribed in square.

import Foundation
import Glibc

// Creating a function to find the area of

// circle inscribed in square
func inscribedCircleArea(q:Double) -> Double{
   return (Double.pi/4) * q * q
}
var num = 10.0
print("Side of the square is", num)
print("Area of the circle inscribe in square:", inscribedCircleArea(q:num))

Output

Side of the square is 10
Area of the circle inscribe in square: 78.53981633974483

Here, in the above program we create a function which return the area of the circle inscribe in the square using the following formula −

return (Double.pi/4) * q * q

Here, Double.pi is used to access predefined pi value.