Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Area of a circle inscribed in a rectangle which is inscribed in a semicircle?
Let us consider one semicircle is given. Its radius is R. One rectangle of length l and breadth b is inscribed in that semi-circle. Now one circle with radius r is inscribed in the rectangle. We have to find the area of the inner circle.
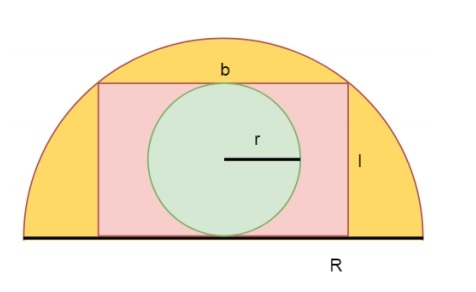
As we know biggest rectangle that can be inscribed within the semi-circle has length l and breadth b, then the equation of l and b will be like following −
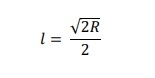
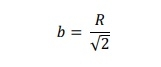
Now, the biggest circle that can be inscribed within the rectangle has radius r is like below −
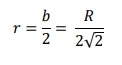
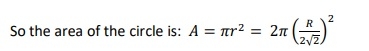
Example
#include <iostream>
#include <cmath>
using namespace std;
float innerCircleArea(float R){
return 3.1415 * pow(R / (2 * sqrt(2)), 2);
}
int main() {
float rad = 12.0f;
cout << "Area: " << innerCircleArea(rad);
}Output
Area: 56.547
Updated on: 31-Jul-2019
76 Views
Advertisements