Application of Integrals

Introduction

Application of Integrals is applied in various fields like Mathematics, Science, Engineering etc. The application of integrals is widely seen in both mathematics and physics for various purposes.

• If integration is applied for an area under a curve or area between two curves it is called the geometrical application of integrals which also includes finding the volume of solid revolution, length of the curve, etc.,

• If the integration is applied to find the centre of gravity, mass, momentum, displacement, the velocity of objects, etc., then it is called the physical application of integrals.

In this tutorial, we will learn about integrals and their applications in the area under the curve and the area between two curves along with a few solved examples.

Integrals

A numerical value equal to the area under a curve or a function can be called an Integral. It is said that they assign values to the functions that explain the area, volume, etc., since they measure the entire space within the provided intervals.

The area A is given by,

$$\mathrm{A = \int_{x=a}^{x=b}f(x) dx}$$

The Integration is called the process of finding these integrals. There are two types of integrals, namely, definite and indefinite integrals. The Integral functions with limits are called definite integrals.

Definite integrals are defined by,

$$\mathrm{I=\int_{x=a}^{x=b}f(x) dx}$$

The Integral functions without limits are called indefinite integrals.

Indefinite integrals are defined by,

$$\mathrm{\int_{x=a}^{x=b}f(x) dx=F(x)+C\: where\: C\: is\: a\: constant.}$$

Application of Integrals: Area under a curve

The area A under the curve f(x) is within the interval [a, b]. We need to integrate f(x) between the limits of a and b to find the A under f(x). Since the integral function has limits a and b, f(x) is said to be a definite integral.

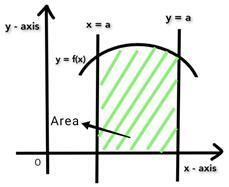
The formula to calculate the area under the curve is given by,

$$\mathrm{A = \int_{x=a}^{x=b}f(x) dx}$$

The Area between two curves

The two curves f(x) and g(x) intersect at two points. The points of intersection are x= a and x=b which obviously we know are x - coordinates. The two curves enclose an area A between them.

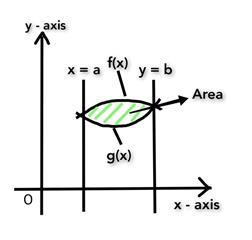
• If the curve f(x) is higher than g(x) such that, f(x) ≤g(x) for a≤ x ≤b then

  the formula for finding the area between two curves is given by,

  $$\mathrm{A = \int_{x=a}^{x=b}f(x) dx-\int_{x=a}^{x=b}g(x) dx}$$

• If the curve g(x) is higher than f(x) such that, g(x) ≤f(x) for a≤ x ≤b then

  the formula for finding the area between two curves is given by,

  $$\mathrm{A = \int_{x=a}^{x=b}g(x) dx-\int_{x=a}^{x=b}f(x) dx}$$

Solved Examples

1)Find the Area A under the curve of the function f(x)=(x⁴+6) and the given limit is 2≤ x ≤3.

Answer:

The formula to calculate the area under the curve is given by,

Area under the curve is = $\mathrm{\int_{x=a}^{x=b}f(x) dx}$

Area under the given curve is = $\mathrm{\int_2^3(x^4+6) dx}$

Area under the given curve is = $\mathrm{[\frac{x^5}{5}+6x]_{x=2}^{x=3}}$

Area under the given curve is = $\mathrm{[\frac{3^5}{5}-\frac{2^5}{5}] +[6(3)-6(2)]}$

Area under the given curve is = $\mathrm{[\frac{243-32}{5}] +[18-12]}$

Area under the given curve is =$\mathrm{\frac{211}{5}+6}$

Area under the given curve is = $\mathrm{\frac{211+30}{5}}$

Area under the given curve is = $\mathrm{\frac{241}{5}}$

Area under the given curve is = 48.1 sq. units.

Therefore, the Area under the curve of the function (x⁴+6) is 48.1 sq. units.

2)Find the Area A between the given two curves f(x)=3x and g(x)=2x the given limit is 0≤ x ≤3.

Answer:

The formula for finding the area between two curves is given by,

Area between the two curves is $\mathrm{= \int_{x=a}^{x=b} f(x) dx-\int_{x=a}^{x=b}g(x) dx}$

Area between the given curves is $\mathrm{= \int_0^3(3x-2x) dx}$

Area between the given curves is = $\mathrm{\int_0^3x dx}$

Area between the given curves is = $\mathrm{[\frac{x^2}{2}]_{x=0}^{x=3}}$

Area between the given curves is = $\mathrm{\frac{(3)^2}{2}-0}$

Area between the given curves is = $\mathrm{\frac{9}{2}}$

Area between the given curves is = 4.5 sq.units.

Therefore, the Area A between the given two curves f(x)=3x and g(x)=2x is 4.5 sq.units.

3)Find the Area A under the curve of the function f(x)=(5x-x^2) and the given limit is 0≤ x ≤5.

Answer:

The formula to calculate the area under the curve is given by,

Area under the curve is = $\mathrm{\int_{x=a}^{x=b}f(x) dx}$

Area under the given curve is = $\mathrm{\int_0^5(5x-x^2) dx}$

Area under the given curve is =$\mathrm{[\frac{5x^2}{2}+\frac{x^3}{3}]_{x=0}^{x=5}}$

Area under the given curve is = $\mathrm{[\frac{5(5)^2}{2}-\frac{5^3}{3}] -0}$

Area under the given curve is = $\mathrm{[\frac{125}{2}-\frac{125}{3}] -0}$

Area under the given curve is = $\mathrm{\frac{(3×125) - (2×125)}{6}}$

Area under the given curve is = $\mathrm{\frac{375 - 250}{6}}$

Area under the given curve is = $\mathrm{\frac{125}{6}}$

Area under the given curve is = 20.833 sq. units.

Therefore, the Area under the curve of the function $\mathrm{\int_0^5(5x-x^2) dx}$ is 20.833 sq.units.

4)Find the Area A between the given two curves f(x)=x⁴ and g(x)=x the given limit is 2≤ x ≤3.

Answer:

The formula for finding the area between two curves is given by,

$$\mathrm{A=\int_{x=a}^{x=b}f(x) dx-\int_{x=a}^{x=b}g(x) dx}$$

$$\mathrm{A=\int_2^3(x^4-x) dx}$$

$$\mathrm{A=[\frac{x^5}{5}-\frac{x^2}{2}]_{x=2}^{x=3}}$$

$$\mathrm{A=[\frac{3^5- 2^5}{5}]-[\frac{3^2-2^2}{2}]}$$

$$\mathrm{A=[\frac{243- 32}{5}]-[\frac{9-4}{2}]}$$

$$\mathrm{A=\frac{211}{5}-\frac{5}{2}}$$

$$\mathrm{A=\frac{422-25}{10}}$$

$$\mathrm{A=\frac{397}{10}}$$

$$\mathrm{A=39.7\: sq.units.}$$

Therefore, the Area A between the given two curves f(x)=x⁴ and g(x)=x is 39.7 sq.units.

Conclusion

• The representations of the areas under the curves are defined as the integrals.

• The definite integral I is given by,

  $$\mathrm{I= \int_{x=a}^{x=b}f(x) dx}$$

• The Integral functions without limits, such that $\mathrm{\int_{x=a}^{x=b}f(x) dx=F(x)+C}$ are called indefinite integrals.

• The formula to calculate the area under the curve is given by,

  $$\mathrm{A =\int_{x=a}^{x=b}f(x) dx}$$

• The formula for finding the area between two curves is given by,

  $$\mathrm{Area=\int_{x=a}^{x=b}[f(x) -g(x)]dx}$$

FAQs

1. Which are considered the important tools of Calculus?

The significant tools of Calculus are integrals, limits, and derivatives.

Their role is to describe the behaviour functions and then analyze them.

History says, in the late 17th century the famous Mathematicians, Sir Issac Newton and Gottfried Leibniz discovered Calculus since they contributed to the development of the theories on derivatives and differentiation.

2. Who introduced integration by parts?

The English Mathematician, Brook Taylor best known for Taylor's series and theorem was the one who discovered integration by parts. Because of this great Mathematician, we have a new branch called the Calculus of finite differences.

3. What is a Surface Integral?

The integrals over curved two-dimensional regions or planes are called surface integrals.

To define the surface integral of function $\mathrm{\underline{F}}$, a whole surface S is divided into small surface elements ΔS.

$$\mathrm{\int▁F⋅ds=\lim_{n \rightarrow ∞} \sum_{i=1}^{n}\underline{F_i}\: \underline{ΔS_i} , \: ΔS→0}$$

4. What is a line integral?

If the function of an integral is calculated along a curve, then that integral is said to be line integral.

It can also be called a path integral.

5. What is the difference between double and surface integrals?

Integrals over a flat two-dimensional plane are double integrals. Whereas Integrals over a curved two-dimensional plane are surface integrals.