Properties of Definite Integrals

Introduction

There are two methods of integration −

• Deterministic integration and

• Indefinite integration.

Definitive integration is performed on boundaries or areas specified by boundaries. Since the curve is finite, the area under the curve is also said to be finite, but indefinite integrals are used for functions that have no upper or lower bound, but because the function is essentially infinite, the upper bound and the lower limit is indefinite. Functions + ∞ & -∞.

Integrals

• In differential calculus we are concerned with the methods of finding the derivative (or differential) of a differentiable function.

• Can we solve the converse problem? That is, if the function having the given derivative (or differential)? For example, the derivative of the function y=x⁶ is $\mathrm{\frac{dy}{dx}=6x^5}$ (or its differential is $\mathrm{dy=6x^5 dx }$). Hence, it is easily understood that the function having derivative $\mathrm{6x^5}$ (or differential $\mathrm{6x^5 dx}$ ) is x⁶ .

• In this case, the mathematical method which determines the function y=x⁶ from the derivative dy/dx=6x^5 (or differential) dy=6x^5 dx is called integration.

• The function obtained by integration from the derivative (or differential) of the function is called its integral. In the above example, the integral of $\mathrm{\frac{dy}{dx}=6x^5}$ (or, $\mathrm{dy=6x^5 dx }$ ) is y=x⁶. Clearly, integration can be looked upon as antiderivative i.e, it is inverse process of differentiation.

Definite Integrals

If a quantity under any mathematical investigation can be expressed in the form of a series by dividing it into several parts according to some law or rule such that the number of terms of the series can be increased indefinitely and each term of the series is infinitesimally small, then the limiting value of the sum of such a series is called a definite integral.

Definite Integrals as Limit of Sums

Let f(x) be a bounded single-valued continuous function defined in the finite interval a≤x≤b. Now, divide the interval a≤x≤b into n equal sub-intervals each of length h by the points a,a+h,a+2 h,….,a+(n-1)h …a+nh where a+nh=b, or nh=b-a. Then the limit (if exists),

$$\mathrm{\displaystyle\lim \limits_{h\rightarrow 0}h[\mathit{f}(a)+\mathit{f}(a+h)+\mathit{f}(a+2h)[\mathit{f}(a)\mathit{f}(a+(n-1)h)]]}$$

or, in short,$\mathrm{\displaystyle\lim \limits_{h\rightarrow 0}h\displaystyle\sum\limits_{r=0}^{n-1}\mathit{f}(a+r h) }$ is called the definite integral of f(x) with respect to x between the limits a and b and is denoted by the symbol .

$$\mathrm{\int_{a}^{b}\mathit{f}(x) d x }$$

Here b is called the upper or superior limit of the integral and a is called its lower or inferior limit. Hence,

$$\mathrm{\int_{a}^{b}\mathit{f}(x) d x =\displaystyle\lim \limits_{h\rightarrow 0}h\displaystyle\sum\limits_{r=0}^{n-1}\mathit{f}(a+r h) }$$

where nh=b-a provided the limit exists.

In mathematics, simple sums and additions are easy, but when it comes to evaluating complex integrals, simple calculations and additions are not enough and integration is needed. When evaluating definite integrals, the calculations can be cumbersome and complex, so use empirically proven properties to make the calculations relatively easy.

Definite Integrals for Area under a Curve

Suppose we want to find the area bounded by the continuous curve y=x², the x-axis, the ordinate x=1 and the ordinate x=4.

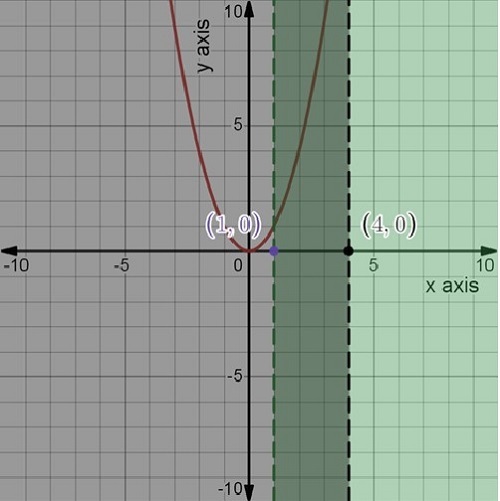
Clearly, the area can be divided into 10 parts by dividing the interval 1≤x≤4 into 10 equal sub-intervals by the points x=1,1.3,1.6,.... and erecting ordinates at each point of sub-division. Hence, the enclosed area can be represented in the form of a series of 10 terms. Similarly, if the interval 1≤x≤4 is divided into 100 equal sub-intervals by the points x=1,1.03,1.06,..... and ordinates are erected at each point of sub-division then the enclosed area can be represented in the form of a series of 100 terms.

Properties of Definite Integrals

The properties of definite integrals are −

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=\int_{a}^{b}\mathit{f}(t) d(t)}$

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=-\int_{b}^{a}\mathit{f}(x) dx}$

• $\mathrm{\int_{a}^{a}\mathit{f}(x) d x=0}$

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=\int_{a}^{c}\mathit{f}(x) d x+\int_{c}^{b}\mathit{f}(x) d x}$

• $\mathrm{\int_{a}^{b}\mathit{f}(x) d x=\int_{a}^{b}\mathit{f}(a + b – x) d x}$

• $\mathrm{\int_{0}^{a}\mathit{f}(x) d x=\int_{a}^{b}\mathit{f}(a – x) d x}$

Solved Examples

1.Evaluate $\mathrm{\int_{1}^{e}\frac{dx}{x(1+logx)^2}}$

Since,

$$\mathrm{\int\frac{dx}{x(1+logx)^2}=-\frac{1}{z}=-\frac{1}{1+logx}}$$

Therefore,$\mathrm{\int_{1}^{e}\frac{dx}{x(1+logx)^2}=-[\frac{1}{1+logx}]_1^e=-[\frac{1}{1+loge}-\frac{1}{1+log1}]=-(\frac{1}{2}-1)=\frac{1}{2}}$

Hence, $\mathrm{\int_{1}^{e}\frac{dx}{x(1+logx)^2}=\frac{1}{2}}$.

2.If $\mathrm{\mathit{f}(x)=\mathit{f}(a+x)}$, then prove that $\mathrm{\int_a^{a+t} \mathit{f}(x)dx }$ is independent of a.

We put, x=a+z; therefore, dx=dz.

Again, z=0, when x=a and z=t when x=a+t.

Therefore,

$\mathrm{ \int_a^{a+t} f(x)dx=\int_0^t f(a+z)dz=\int_0^t f(a+x)dx=\int_0^t f(x)dx }$ and it is independent of a.

Hence, proved.

3.Evaluate the following definite integral: $\mathrm{ \int_{-a}^a \frac{dx}{x^a+a^2}}$.

$$\mathrm{\int_{-a}^a \frac{dx}{x^a+a^2}=\frac{1}{a}[tan^{-1} \frac{x}{a}]^a_{-a}=\frac{1}{a}[tan^{-1} \frac{a}{a}-tan^{-1} \frac{-a}{a}]}$$

$$\mathrm{=\frac{1}{a}[tan^{-1} 1-tan^{-1} (-1)]=\frac{1}{a}[\frac{π}{4}-(-\frac{π}{4})]=\frac{π}{2a}}$$

Hence, $\mathrm{\int_{-a}^a \frac{ dx}{x^a+a^2}=\frac{π}{2a}}$

Conclusion

Integration, as the name implies, is used to integrate something. In mathematics, integration is a method of integrating a function. Another term for integrals could be a sum, or a graphical way to find the area under a curve function, used to summarize the entire function. The integral is known to be the opposite of the derivative, the function is decomposed into smaller functions, and the integral sums the smaller bits to get the total area under the curve. The enclosed area in the form of a series whose number of terms can be made larger and larger and the value of each term becomes smaller and smaller. In this case, the limiting value of the sum of such a series is called a definite integral.

FAQs

1. What is a definite integral?

The definite integral defines the area below the curve between the two fixed limits. This is expressed as ∫a.0f (x) dx. Where and are the lower and upper bounds of the function f (x) defined for the x-axis, respectively.

2. How do you evaluate the definite integral?

The definite integral is evaluated as follows.

Step 1: Find the integral of the indefinite integral.

Step 2: Apply limits to the result

Step 3: Substitute the upper and lower bounds and subtract the value obtained.

3.What are the first things to consider when evaluating a particular integral?

To evaluate a definite integral, you must first evaluate the indefinite integral of the function. Therefore, the first thing to consider when evaluating a definite integral is to take a definite integral and do the integral.

4. How do you evaluate the definite integral graphically?

The evaluation of the definite integral is to find the area below the curve. To find the area below the curve between the two boundaries, divide the area into rectangles and sum those areas. The more rectangles, the more accurate the area. Therefore, divide the area into an infinite number of rectangles, each of the same (very small) size, and sum all the areas.

5. How is the definition integral evaluated?

Definite integrals are evaluated using various methods. The various ways to evaluate definite integrals are −

• Basic analysis theorem

• Evaluation of definite integral by substitution

• Evaluation of definite integral by graph

• Evaluation of definite integral by geometry

• Evaluation of definite integral by property

6. What is the purpose of definite integral?

Some applications of definite integrals are −

• You can use the definite integral to find the area below the curve and the area between the two curves.

• The volume of a 3D object can be determined using a definite integral.

• Use the definite integral to calculate the arc length of the curve.

• Force function integration can also be used to determine work.

• The force exerted on an object immersed in a liquid can also be calculated using a definite integral.