Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
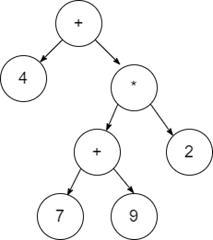
Algorithm to construct an Expression Tree in Data Structure
Expression trees
Expression trees are those in which the leaf nodes have the values to be operated, and internal nodes contain the operator on which the leaf node will be performed.
Example
4 + ((7 + 9) * 2) will have an expression tree as follows
Algorithm to Construct an Expression Tree
Let T be the expression tree.
If T is not NULL:
If T->data is an operand:
return T.data
A = solve(T.left)
B = solve(T.right)
--> Calculate operator for 'T.data' on A and B, and call recursively,
return calculate(A, B, T.data)
How to construct an expression tree?
To construct an Expression Tree for the given expression, we generally use Stack Data Structure.
Initially we Iterate over the given postfix expression and follow the steps as given below -
- If we get an operand in the given expression, then push it in the stack. It will become the root of the expression Tree.
- If an operator gets two values in the expression, then add in the expression tree as its child, and push them in the current node.
- Repeat Step-1 and Step-2 until we do not complete over the given expression.
- Now check if every root node contains nothing but operands and every child node contains only values.
Updated on: 23-Feb-2021
7K+ Views
Advertisements