
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Python Program to Construct an Expression Tree of a given Expression
Expression trees are those in which the leaf nodes have the values to be operated, and the internal nodes contain the operator on which the leaf node will be performed.
Example: 4 + ((7 + 9) * 2) will have an expression tree like -
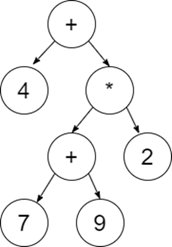
Approach to solve this Problem
In order to construct an Expression Tree for a given expression, we generally use Stack Data Structure. Initially we Iterate over the given postfix expression and follow the steps as given below -
- If we get an operand in the given expression, then push it in the stack. It will become the root of the expression Tree.
- If an operator gets two values in the expression, then add in the expression tree as its child, and push them in the current node.
- Repeat Step-1 and Step-2 until we don't complete over our given expression.
Example
class stack: def __init__(self): self.arr = [] def push(self, data): self.arr.append(data) def pop(self): try: return self.arr.pop(-1) except: pass def top(self): try: return self.arr[-1] except: pass def size(self): return len(self.arr) # node class for expression tree class node: def __init__(self, data): self.data = data self.left = None self.right = None # expression tree class class exp_tree: def __init__(self, postfix_exp): self.exp = postfix_exp self.root = None self.createTree(self.exp) def isOperator(self, char): optr = [" ", "-", "*", "/", "^"] if char in optr: # if given char is operator return True # then return true return False # else return false def createTree(self, exp): s = stack() # store those operator node whose any child node is NULL self.root = node(exp[-1]) # last character of postfix expression is always an operator s.push(self.root) # travel on rest of the postfix expression for i in "".join(reversed(exp[:-1])): curr_node = s.top() if not curr_node.right: # if right node of current node is NULL temp = node(i) curr_node.right = temp if self.isOperator(i): s.push(temp) else: # if left node of current node is NULL temp = node(i) curr_node.left = temp # if no child node of current node is NULL s.pop() # pop current from stack if self.isOperator(i): s.push(temp) def inorder(self, head): # inorder traversal of expression tree # inorder traversal = > left, root, right if head.left: self.inorder(head.left) print(head.data, end=" ") if head.right: self.inorder(head.right) def infixExp(self): # inorder traversal of expression tree give infix expression self.inorder(self.root) print() if __name__ == "__main__": postfixExp = "ab ef*g*-" et = exp_tree(postfixExp) et.infixExp()
Running the above code will generate the output as,
Output
(a + b - e * f * g)
Explanation:
Constructing a tree from a given expression will generate the output such that the operand will become the root of the node and the rest of the numbers will become the child nodes of the expression tree.

Advertisements
