Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Pendent Vertex, Isolated Vertex and Adjacency of a graph
Pendent Vertex
By using degree of a vertex, we have a two special types of vertices. A vertex with degree one is called a pendent vertex.
Example
Here, in this example, vertex 'a' and vertex 'b' have a connected edge 'ab'. So with respect to the vertex 'a', there is only one edge towards vertex 'b' and similarly with respect to the vertex 'b', there is only one edge towards vertex 'a'. Finally, vertex 'a' and vertex 'b' has degree as one which are also called as the pendent vertex.
Isolated Vertex
A vertex with degree zero is called an isolated vertex.
Example
Here, the vertex 'a' and vertex 'b' has a no connectivity between each other and also to any other vertices. So the degree of both the vertices 'a' and 'b' are zero. These are also called as isolated vertices.
Adjacency
Here are the norms of adjacency −
In a graph, two vertices are said to be adjacent, if there is an edge between the two vertices. Here, the adjacency of vertices is maintained by the single edge that is connecting those two vertices.
In a graph, two edges are said to be adjacent, if there is a common vertex between the two edges. Here, the adjacency of edges is maintained by the single vertex that is connecting two edges.
Example 1
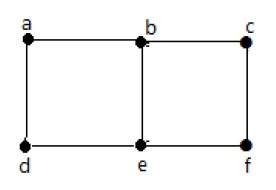
In the above graph −
'a' and 'b' are the adjacent vertices, as there is a common edge 'ab' between them.
'a' and 'd' are the adjacent vertices, as there is a common edge 'ad' between them.
ab' and 'be' are the adjacent edges, as there is a common vertex 'b' between them.
be' and 'de' are the adjacent edges, as there is a common vertex 'e' between them.
Example 2
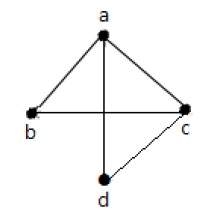
In the above graph −
'a' and 'd' are the adjacent vertices, as there is a common edge 'ad' between them.
'c' and 'b' are the adjacent vertices, as there is a common edge 'cb' between them.
'ad' and 'cd' are the adjacent edges, as there is a common vertex 'd' between them.
ac' and 'cd' are the adjacent edges, as there is a common vertex 'c' between them.
6K+ Views
