Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Dijkstra’s Algorithm for Adjacency List Representation
There is a given graph G(V, E) with its adjacency list representation, and a source vertex is also provided. Dijkstra’s algorithm to find the minimum shortest path between source vertex to any other vertex of the graph G.
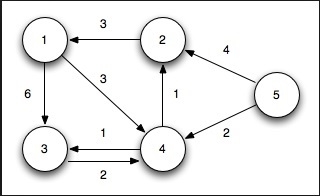
To Solve this problem, we will use two lists. One is to store vertices which have been considered as the shortest path tree, and another will hold the vertices which are not considered yet. In each phase of the algorithm, we find the unconsidered vertex and which has the minimum distance from the source.
Another list is used to hold the predecessor node. Using the predecessor node, we can find the path from source and destination.
The complexity of Dijkstra’s shortest path algorithm is O(E log V) as the graph is represented using adjacency list. Here the E is the number of edges, and V is Number of vertices.
Input and Output
Input: The adjacency list of the graph with the cost of each edge.Output: 0 to 1, Cost: 3 Previous: 0 0 to 2, Cost: 5 Previous: 1 0 to 3, Cost: 4 Previous: 1 0 to 4, Cost: 6 Previous: 3 0 to 5, Cost: 7 Previous: 2 0 to 6, Cost: 7 Previous: 4
Algorithm
dijkstraShortestPath(g : Graph, dist, prev, start : node)
Input − The graph g, dist list to store distance, prev list for predecessor nodes, and start vertex.
Output − The shortest paths from start to all other vertices.
Begin for all vertices u in (V - start) do dist[u] := ∞ prev[u] := φ done set dist[start] = 0 and prev[start] := φ for all node u in V do insert u into queue ‘Q’. done while Q is not empty do u := minimum element from Queue delete u from Q insert u into set S for each node v adjacent with node u do if dist[u]+cost(v) < dist[v] then dist[v] := dist[u]+cost(v) prev[v] := u done done End
Example
#include<iostream>
#include<set>
#include<list>
#include<algorithm>
using namespace std;
typedef struct nodes {
int dest;
int cost;
}node;
class Graph {
int n;
list<node> *adjList;
private:
void showList(int src, list<node> lt) {
list<node> :: iterator i;
node tempNode;
for(i = lt.begin(); i != lt.end(); i++) {
tempNode = *i;
cout << "(" << src << ")---("<<tempNode.dest << "|"<<tempNode.cost<<") ";
}
cout << endl;
}
public:
Graph() {
n = 0;
}
Graph(int nodeCount) {
n = nodeCount;
adjList = new list<node>[n];
}
void addEdge(int source, int dest, int cost) {
node newNode;
newNode.dest = dest;
newNode.cost = cost;
adjList[source].push_back(newNode);
}
void displayEdges() {
for(int i = 0; i<n; i++) {
list<node> tempList = adjList[i];
showList(i, tempList);
}
}
friend void dijkstra(Graph g, int *dist, int *prev, int start);
};
void dijkstra(Graph g, int *dist, int *prev, int start) {
int n = g.n;
for(int u = 0; u<n; u++) {
dist[u] = 9999; //set as infinity
prev[u] = -1; //undefined previous
}
dist[start] = 0; //distance of start is 0
set<int> S; //create empty set S
list<int> Q;
for(int u = 0; u<n; u++) {
Q.push_back(u); //add each node into queue
}
while(!Q.empty()) {
list<int> :: iterator i;
i = min_element(Q.begin(), Q.end());
int u = *i; //the minimum element from queue
Q.remove(u);
S.insert(u); //add u in the set
list<node> :: iterator it;
for(it = g.adjList[u].begin(); it != g.adjList[u].end();it++) {
if((dist[u]+(it->cost)) < dist[it->dest]) { //relax (u,v)
dist[it->dest] = (dist[u]+(it->cost));
prev[it->dest] = u;
}
}
}
}
main() {
int n = 7;
Graph g(n);
int dist[n], prev[n];
int start = 0;
g.addEdge(0, 1, 3);
g.addEdge(0, 2, 6);
g.addEdge(1, 0, 3);
g.addEdge(1, 2, 2);
g.addEdge(1, 3, 1);
g.addEdge(2, 1, 6);
g.addEdge(2, 1, 2);
g.addEdge(2, 3, 1);
g.addEdge(2, 4, 4);
g.addEdge(2, 5, 2);
g.addEdge(3, 1, 1);
g.addEdge(3, 2, 1);
g.addEdge(3, 4, 2);
g.addEdge(3, 6, 4);
g.addEdge(4, 2, 4);
g.addEdge(4, 3, 2);
g.addEdge(4, 5, 2);
g.addEdge(4, 6, 1);
g.addEdge(5, 2, 2);
g.addEdge(5, 4, 2);
g.addEdge(5, 6, 1);
g.addEdge(6, 3, 4);
g.addEdge(6, 4, 1);
g.addEdge(6, 5, 1);
dijkstra(g, dist, prev, start);
for(int i = 0; i<n; i++)
if(i != start)
cout<<start<<" to "<<i<<", Cost: "<<dist[i]<<" Previous: "<<prev[i]<<endl;
}Output
0 to 1, Cost: 3 Previous: 0 0 to 2, Cost: 5 Previous: 1 0 to 3, Cost: 4 Previous: 1 0 to 4, Cost: 6 Previous: 3 0 to 5, Cost: 7 Previous: 2 0 to 6, Cost: 7 Previous: 4
4K+ Views
