
- Java Data Structures Resources
- Java Data Structures - Quick Guide
- Java Data Structures - Resources
- Java Data Structures - Discussion
Breadth-first search (BFS)
A graph is a pictorial representation of a set of objects where some pairs of objects are connected by links. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are called edges.
Formally, a graph is a pair of sets (V, E), where V is the set of vertices and E is the set of edges, connecting the pairs of vertices. Take a look at the following graph −
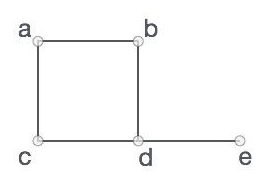
In the above graph,
V = {a, b, c, d, e}
E = {ab, ac, bd, cd, de}
Breadth-first search (BFS)
Breadth First Search (BFS) algorithm traverses a graph in a breadth ward motion and uses a queue to remember to get the next vertex to start a search, when a dead end occurs in any iteration.
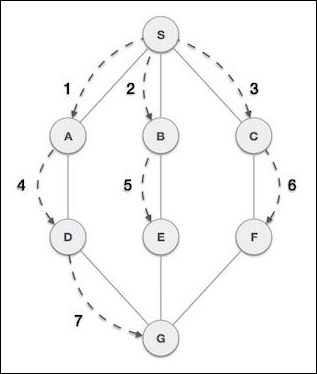
As in the example given above, BFS algorithm traverses from A to B to E to F first then to C and G lastly to D. It employs the following rules.
Rule 1 − Visit the adjacent unvisited vertex. Mark it as visited. Display it. Insert it in a queue.
Rule 2 − If no adjacent vertex is found, remove the first vertex from the queue.
Rule 3 − Repeat Rule 1 and Rule 2 until the queue is empty.
| Step | Traversal | Description |
|---|---|---|
| 1 | 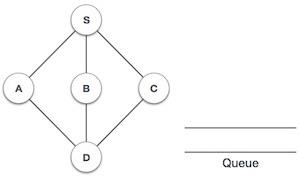 |
Initialize the queue. |
| 2 | 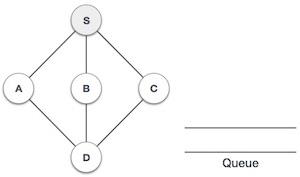 |
We start from visiting S (starting node), and mark it as visited. |
| 3 | 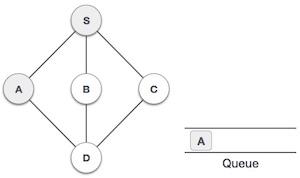 |
We then see an unvisited adjacent node from S. In this example, we have three nodes but alphabetically we choose A, mark it as visited and enqueue it. |
| 4 | 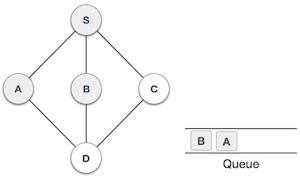 |
Next, the unvisited adjacent node from S is B. We mark it as visited and enqueue it. |
| 5 | 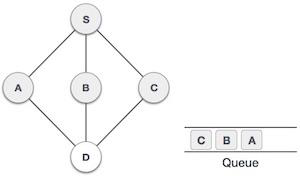 |
Next, the unvisited adjacent node from S is C. We mark it as visited and enqueue it. |
| 6 | 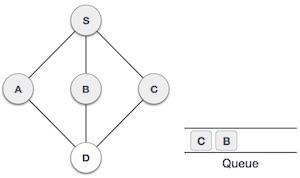 |
Now, S is left with no unvisited adjacent nodes. So, we dequeue and find A. |
| 7 | 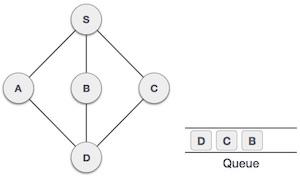 |
From A we have D as unvisited adjacent node. We mark it as visited and enqueue it. |
At this stage, we are left with no unmarked (unvisited) nodes. But as per the algorithm we keep on de-queuing in order to get all unvisited nodes. When the queue gets emptied, the program is over.