
- 3d Figures and Volumes
- Home
- Classifying Solids
- Vertices, Edges, and Faces of a Solid
- Volume of a Rectangular Prism
- Volume of a Rectangular Prism made of Unit Cubes
- Volume of a Solid made of Cubes with Unit Fraction Edge Lengths
- Volume of a Rectangular Prism with Fractional Edge Lengths
- Word Problem Involving the Volume of a Rectangular Prism
- Word Problem Involving the Rate of Filling or Emptying a Rectangular Prism
- Volume of a Triangular Prism
- Word Problem Involving the Volume of a Triangular Prism
Volume of Triangular Prism
Introduction
In this lesson we find the volume of a triangular prism
A triangular prism is a prism that has two congruent parallel triangles as its bases and rectangular lateral faces.
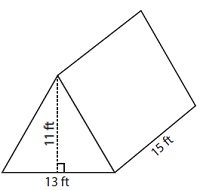
Formula for the volume of a triangular prism
If A is the area of the base triangle and h is the height of the prism then volume of the prism is given by
Volume V = A × h
Where A = $\frac{1}{2}$ b h or $\sqrt{s(s-a)(s-b)(s-c)}$ or $a^2 \sqrt{3}/ 4$
b is the base of the triangle and h is the height
a, b, and c are the sides of the triangle and s =(a+b+c)/2
a is the side of an equilateral triangle
Example 1
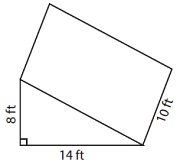
Find the volume of the following triangular prism.
Solution
Step 1:
Volume of a triangular prism = Areas of base triangle × height of prism
Step 2:
Volume of given prism V = $\frac{1}{2}$ × 14 × 8 × 10
= 560 cubic feet
Example 2
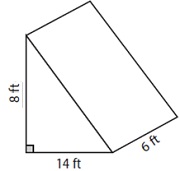
Find the volume of the following triangular prism.
Solution
Step 1:
Volume of a triangular prism = Areas of base triangle × height of prism
Step 2:
Volume of given prism V = $\frac{1}{2}$ × 14 × 8 × 6
= 336 cubic ft