
- 3d Figures and Volumes
- Home
- Classifying Solids
- Vertices, Edges, and Faces of a Solid
- Volume of a Rectangular Prism
- Volume of a Rectangular Prism made of Unit Cubes
- Volume of a Solid made of Cubes with Unit Fraction Edge Lengths
- Volume of a Rectangular Prism with Fractional Edge Lengths
- Word Problem Involving the Volume of a Rectangular Prism
- Word Problem Involving the Rate of Filling or Emptying a Rectangular Prism
- Volume of a Triangular Prism
- Word Problem Involving the Volume of a Triangular Prism
Volume of a Rectangular Prism made of Unit Cubes
Introduction
A unit cube has a length of 1 unit, width of 1 unit and height of 1 unit. Its volume is 1 cubic unit.
Any solid shape can be shown as being of made of unit cubes. Counting the number of unit cubes in that solid shape gives its volume. The cube shaded green is a unit cube.
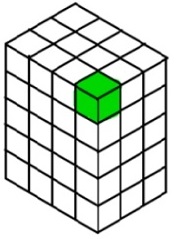
Definition of volume: The number or amount of cubic units it takes to fill a defined space is called volume.
Formula for the volume of a rectangular prism
The volume of a rectangular prism of length l, width w and height h is given by the formula.
The volume of a rectangular prism is given by the product of length, width and the height h of the prism.
Volume V = l × w × h cubic units
Example 1
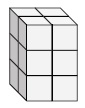
Find the length, width and height of the following rectangular prism. Then find its volume.
Solution
Step 1:
The given prism has length = 2; width = 3; height = 2
Step 2:
The volume of prism V = l × w × h
= 2 × 3 × 2
= 12 cubic units.
Example 2
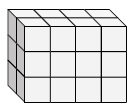
Find the length, width and height of the following rectangular prism. Then find its volume.
Solution
Step 1:
The given prism has length = 4; width = 3; height = 2
Step 2:
The volume of prism V = l × w × h
= 4 × 3 × 2
= 24 cubic units.