
- 3d Figures and Volumes
- Home
- Classifying Solids
- Vertices, Edges, and Faces of a Solid
- Volume of a Rectangular Prism
- Volume of a Rectangular Prism made of Unit Cubes
- Volume of a Solid made of Cubes with Unit Fraction Edge Lengths
- Volume of a Rectangular Prism with Fractional Edge Lengths
- Word Problem Involving the Volume of a Rectangular Prism
- Word Problem Involving the Rate of Filling or Emptying a Rectangular Prism
- Volume of a Triangular Prism
- Word Problem Involving the Volume of a Triangular Prism
Volume of a Rectangular Prism with Fractional Edge Lengths Online Quiz
Following quiz provides Multiple Choice Questions (MCQs) related to Volume of a Rectangular Prism with Fractional Edge Lengths. You will have to read all the given answers and click over the correct answer. If you are not sure about the answer then you can check the answer using Show Answer button. You can use Next Quiz button to check new set of questions in the quiz.

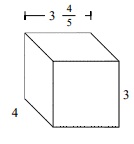
Answer : C
Explanation
Step 1:
The given prism has length = $3 \frac{4}{5}$; width = 4; height = 3
Step 2:
The volume of prism V = l × w × h
= $3 \frac{4}{5}$ × 4 × 3
= $45 \frac{3}{5}$ cubic units.
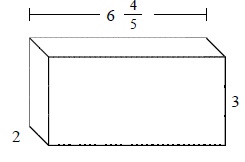
Answer : D
Explanation
Step 1:
The given prism has length = $6 \frac{4}{5}$; width = 2; height = 3
Step 2:
The volume of prism V = l × w × h
= $6 \frac{4}{5}$ × 2 × 3
= $40 \frac{4}{5}$ cubic units.
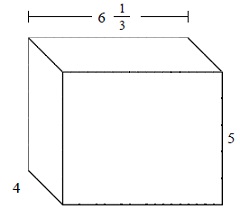
Answer : B
Explanation
Step 1:
The given prism has length = $6 \frac{1}{3}$; width = 4; height = 5
Step 2:
The volume of prism V = l × w × h
= $6 \frac{1}{3}$ × 4 × 5
= $126 \frac{2}{3}$ cubic units.
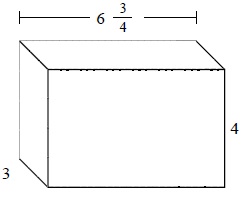
Answer : A
Explanation
Step 1:
The given prism has length = $6 \frac{3}{4}$; width = 3; height = 4
Step 2:
The volume of prism V = l × w × h
= $6 \frac{3}{4}$ × 3 × 4
= 81 cubic units.
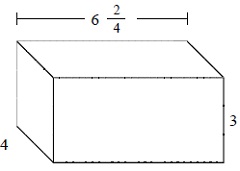
Answer : C
Explanation
Step 1:
The given prism has length = $6 \frac{2}{4}$; width = 4; height = 3
Step 2:
The volume of prism V = l × w × h
= $6 \frac{2}{4}$ × 4 × 3
= 78 cubic units.
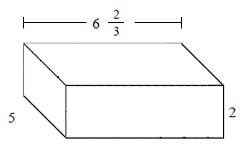
Answer : A
Explanation
Step 1:
The given prism has length = $6 \frac{2}{3}$; width = 5; height = 2
Step 2:
The volume of prism V = l × w × h
= $6 \frac{2}{3}$ × 5 × 2
= $66 \frac{2}{3}$ cubic units.
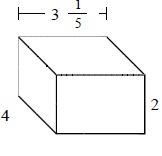
Answer : D
Explanation
Step 1:
The given prism has length = $3 \frac{1}{5}$; width = 4; height = 2
Step 2:
The volume of prism V = l × w × h
= $3 \frac{1}{5}$ × 4 × 2
= $25 \frac{3}{5}$ cubic units.
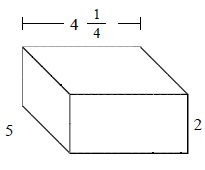
Answer : B
Explanation
Step 1:
The given prism has length = $4 \frac{1}{4}$; width = 5; height = 2
Step 2:
The volume of prism V = l × w × h
= $4 \frac{1}{4}$ × 5 × 2
= $42 \frac{1}{2}$ cubic units.
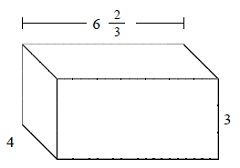
Answer : C
Explanation
Step 1:
The given prism has length = $6 \frac{2}{3}$; width = 4; height = 3
Step 2:
The volume of prism V = l × w × h
= $6 \frac{2}{3}$ × 4 × 3
= 80 cubic units.
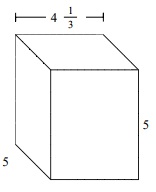
Answer : A
Explanation
Step 1:
The given prism has length = $4 \frac{1}{3}$; width = 5; height = 5
Step 2:
The volume of prism V = l × w × h
= $4 \frac{1}{3}$ × 5 × 5
= $108 \frac{1}{3}$ cubic units.