
- 3d Figures and Volumes
- Home
- Classifying Solids
- Vertices, Edges, and Faces of a Solid
- Volume of a Rectangular Prism
- Volume of a Rectangular Prism made of Unit Cubes
- Volume of a Solid made of Cubes with Unit Fraction Edge Lengths
- Volume of a Rectangular Prism with Fractional Edge Lengths
- Word Problem Involving the Volume of a Rectangular Prism
- Word Problem Involving the Rate of Filling or Emptying a Rectangular Prism
- Volume of a Triangular Prism
- Word Problem Involving the Volume of a Triangular Prism
Volume of a Rectangular Prism with Fractional Edge Lengths
Introduction
In this lesson, we find the volume of rectangular prisms with fractional edge lengths.
Formula for the volume of solid made of cubes with unit fractional edge lengths
l = number of cubes with unit fractional edge length along the length
w = number of cubes with unit fractional edge length along the width
h = number of cubes with unit fractional edge length along the height
k = unit fractional edge length
Volume of solid = l × k × w × k × h × k cubic units
Example 1
Find the volume of following solid of cubes with unit fraction edge lengths. Each prisms unit is measured in cm (not to scale)
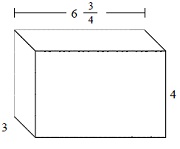
Solution
Step 1:
Solid of cubes with unit fraction edge lengths
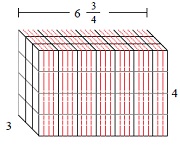
Step 2:
Volume V = l w h = $6 \frac{3}{4} \times 3 \times 4$
= $9 \times \frac{3}{4} \times 4 \times \frac{3}{4} \times \frac{16}{3} \times \frac{3}{4}$
= 81 cu cm
Example 2
Find the volume of following solid of cubes with unit fraction edge lengths. Each prisms unit is measured in cm (not to scale)
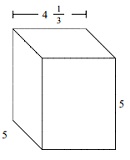
Solution
Step 1:
Solid of cubes with unit fraction edge lengths
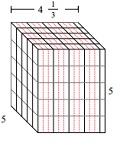
Step 2:
Volume V = l w h = $4 \frac{1}{3} \times 5 \times 5$
= $13 \times \frac{1}{3} \times 15 \times \frac{1}{3} \times 15 \times \frac{1}{3}$
= $108 \frac{1}{3}$ cu cm