
- 3d Figures and Volumes
- Home
- Classifying Solids
- Vertices, Edges, and Faces of a Solid
- Volume of a Rectangular Prism
- Volume of a Rectangular Prism made of Unit Cubes
- Volume of a Solid made of Cubes with Unit Fraction Edge Lengths
- Volume of a Rectangular Prism with Fractional Edge Lengths
- Word Problem Involving the Volume of a Rectangular Prism
- Word Problem Involving the Rate of Filling or Emptying a Rectangular Prism
- Volume of a Triangular Prism
- Word Problem Involving the Volume of a Triangular Prism
Volume of Rectangular Prism
Definitions
Prism
A prism is a solid bounded by a number of plane faces; its two faces, called the ends or bases, are congruent parallel plane polygons and other faces, called the side faces (or lateral faces), and are rectangles.
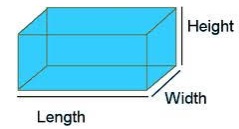
Rectangular Prism
In a rectangular prism the bases or ends are rectangular faces and the lateral faces or side faces are also rectangles.
Formula for the volume of a rectangular prism
The volume of a rectangular prism of length l, width w and height h is given by the formula
The product of the length and width of the base of the rectangular prism gives the area of the base A = l × w
The volume of the rectangular prism is given by the product of area of base A and the height h of the prism.
Volume V = A × h = l × w × h cubic units
Example 1
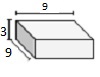
Find the volume of the given rectangular prism in cubic cm.
Solution
Step 1:
Volume of rectangular prism = l × w × h cubic units.
Step 2:
l = 9 cm; w = 3 cm; h = 9 cm
Volume of given prism = 9 × 3 × 9
= 243 cubic cm.
Example 2
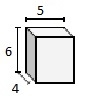
Find the volume of the given rectangular prism in cubic cm.
Solution
Step 1:
Volume of rectangular prism = l × w × h cubic units
Step 2:
l = 5 cm; w = 6 cm; h = 4 cm
Volume of given prism = 5 × 6 × 4
= 120 cubic cm.